题目内容
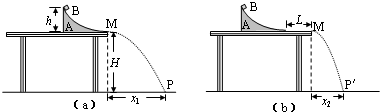
13.某研究小组设计了一种“用一把尺子测定动摩擦因数”的实验方案.如图所示,A是可固定于水平桌面上任意位置的滑槽(滑槽末端与桌面相切),B是质量为m的滑块(可视为质点).第一次实验,如图(a)所示,将滑槽末端与桌面右端M对齐并固定,让滑块从滑槽最高点由静止滑下,最终落在水平地面上的P点,测出滑槽最高点距离桌面的高度h、M距离地面的高度H、M与P间的水平距离x1;
第二次实验,如图(b)所示,将滑槽沿桌面向左移动一段距离并固定,让滑块B再次从滑槽最高点由静止滑下,最终落在水平地面上的P′点,测出滑槽末端与桌面右端M的距离L、M与P′间的水平距离x2.
(1)在第二次实验中,滑块到M点的速度大小为x2$\sqrt{\frac{g}{2H}}$.(用实验中所测物理量的符号表示,已知重力加速度为g).
(2)(多选)通过上述测量和进一步的计算,可求出滑块与桌面间的动摩擦因数μ,下列能引起实验误差的是BCD.(选填序号)
A.h的测量 B.H的测量 C.L的测量 D.x2的测量
(3)若实验中测得h=15cm、H=25cm、x1=30cm、L=10cm、x2=20cm,则滑块与桌面间的动摩擦因数μ=0.5.(结果保留1位有效数字)
分析 (1)由平抛运动的知识求得速度的大小.
(2)凡影响到速度大小的求解的量均会引起实验误差.
(3)先列出μ的表达式,代入数据计算即可.
解答 解:(1)滑块在滑槽末端时的速度大小为:v1=$\frac{{x}_{1}}{t}$;${v}_{2}=\frac{{x}_{2}}{t}$
由竖直方向有:$H\\;=\frac{1}{2}g{t}^{2}$
由①②式求得:v1=x1$\sqrt{\frac{g}{2H}}$
(2)第二次测的速度为:v2=x2$\sqrt{\frac{g}{2H}}$
物体在水平桌面上运动,由动能定理:$-μmgL=\frac{1}{2}{mv}_{2}^{2}-\frac{1}{2}{mv}_{1}^{2}$
由③④⑤式可得:$μ=\frac{{x}_{1}^{2}{-x}_{2}^{2}}{4HL}$ 由表达式可知会引起误差的是BCD.故选:BCD
(3)由$μ=\frac{{x}_{1}^{2}{-x}_{2}^{2}}{4HL}$=$\frac{0.{3}^{2}-0.{2}^{2}}{4×0.25×0.1}$=0.5
故答案为:(1)x2$\sqrt{\frac{g}{2H}}$( 2)BCD (3)0.5
点评 该实验有一定的创新性,其实很多复杂的实验其实验原理都是来自我们所学的基本规律,这点要在平时训练中去体会

练习册系列答案
相关题目
4.据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的6.4倍,一个在地球表面重量为600N的人在这个行星表面的重量将变为960N,由此可推知该行星的半径与地球半径之比约为( )
| A. | 1:2 | B. | 2:1 | C. | 3:2 | D. | 4:1 |
8. 一质量为0.5kg的物体受到一竖直方向拉力F的作用向上做直线运动,假定物体开始时所在平面为零势能面,机械能E随位移h的变化规律如图所示,重力加速度g取10m/s2,整个过程空气阻力不计.下列关于物体的运动情况说法正确的是( )
一质量为0.5kg的物体受到一竖直方向拉力F的作用向上做直线运动,假定物体开始时所在平面为零势能面,机械能E随位移h的变化规律如图所示,重力加速度g取10m/s2,整个过程空气阻力不计.下列关于物体的运动情况说法正确的是( )
 一质量为0.5kg的物体受到一竖直方向拉力F的作用向上做直线运动,假定物体开始时所在平面为零势能面,机械能E随位移h的变化规律如图所示,重力加速度g取10m/s2,整个过程空气阻力不计.下列关于物体的运动情况说法正确的是( )
一质量为0.5kg的物体受到一竖直方向拉力F的作用向上做直线运动,假定物体开始时所在平面为零势能面,机械能E随位移h的变化规律如图所示,重力加速度g取10m/s2,整个过程空气阻力不计.下列关于物体的运动情况说法正确的是( )| A. | 0.5m~2.5m过程,物体做匀速直线运动 | |
| B. | 0.5m~2.5m过程,物体做匀加速直线运动 | |
| C. | 2.5m~3m过程,物体的加速度大小为10m/s2 | |
| D. | 物体上升过程中拉力F方向一直保持竖直向上 |
18.据报道,我国将于2016年择机发射“天宫二号”,并计划于2020年发射“火星探测器”.设“天宫二号”绕地球做圆周运动的半径为r1、周期为T1;“火星探测器”绕火星做做圆周运动的半径为r2、周期为T2,万有引力常量为G.根据题设条件可得( )
| A. | 关系式$\frac{{{r}_{1}}^{3}}{{{T}_{1}}^{2}}$=$\frac{{{r}_{2}}^{3}}{{{T}_{2}}^{2}}$ | |
| B. | 地球与火星的平均密度之比为$\frac{{{T}_{1}}^{2}}{{{T}_{2}}^{2}}$ | |
| C. | 地球与火星的质量之比为$\frac{{{r}_{1}}^{3}{{T}_{2}}^{2}}{{{r}_{2}}^{3}{{T}_{1}}^{2}}$ | |
| D. | “天宫二号”和“火星探测器”的向心加速度大小之比为$\frac{{r}_{1}{{T}_{2}}^{2}}{{r}_{2}{{T}_{1}}^{2}}$ |
5.A、B两颗卫星围绕地球做匀速圆周运动,A卫星运行的周期为T1,轨道半径为r1;B卫星运行的周期为T2,且T1>T2.下列说法正确的是( )
| A. | B卫星的轨道半径为r1($\frac{{T}_{1}}{{T}_{2}}$)${\;}^{\frac{2}{3}}$ | |
| B. | A卫星的机械能一定大于B卫星的机械能 | |
| C. | 某时刻卫星A、B在轨道上相距最近,从该时刻起每经过$\frac{{T}_{1}{T}_{2}}{{T}_{1}-{T}_{2}}$时间,卫星A、B再次相距最近 | |
| D. | A、B卫星在轨道上运行时处于完全失重状态,不受任何力的作用 |
 一位同学利用光电加速器等器材做实验来验证自由落体运动是匀变速直线运动,如图甲所示,该同学让一直径为d、质量为m的金属小球从O处由静止释放,下落过程中能通过O处正下方,固定于M处的光电门,测得O、M间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g.
一位同学利用光电加速器等器材做实验来验证自由落体运动是匀变速直线运动,如图甲所示,该同学让一直径为d、质量为m的金属小球从O处由静止释放,下落过程中能通过O处正下方,固定于M处的光电门,测得O、M间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g. 如图所示,闭合线圈abcd竖直放置在匀强磁场中,线圈的匝数为100匝.开始时线圈静止不动,然后线圈从图示位置绕转动轴OO′旋转90°,所用时间为0.5s,穿过线圈的磁通量变化量为0.08Wb.问:
如图所示,闭合线圈abcd竖直放置在匀强磁场中,线圈的匝数为100匝.开始时线圈静止不动,然后线圈从图示位置绕转动轴OO′旋转90°,所用时间为0.5s,穿过线圈的磁通量变化量为0.08Wb.问: 如图所示,容积为V0的光滑圆柱形气缸竖直放置,用质量不计的活塞将一定质量的理想气体和一固体封闭在气缸内.气缸内设有卡环ab,卡环位于气缸深度一半的位置.开始时活塞位于气缸顶部,将一小盒沙子缓慢地倒在活塞的上表面.活塞最终下降到气缸深度五分之四的位置,再将相同质量的9小盒沙子缓慢地倒在活塞的上表面,活塞最终刚好降至卡环处,又将同样四小盒沙子倒在活塞的上表面,然后缓慢加热气缸.已知大气压强为p0,气体初始温度为T0.试求:
如图所示,容积为V0的光滑圆柱形气缸竖直放置,用质量不计的活塞将一定质量的理想气体和一固体封闭在气缸内.气缸内设有卡环ab,卡环位于气缸深度一半的位置.开始时活塞位于气缸顶部,将一小盒沙子缓慢地倒在活塞的上表面.活塞最终下降到气缸深度五分之四的位置,再将相同质量的9小盒沙子缓慢地倒在活塞的上表面,活塞最终刚好降至卡环处,又将同样四小盒沙子倒在活塞的上表面,然后缓慢加热气缸.已知大气压强为p0,气体初始温度为T0.试求: