题目内容
14. 如图所示xoy平面内,y≥5cm和y<0的范围内存在匀强磁场,磁场方向垂直纸面向里,磁感应强度均为B=1.0T,一个质量为m=1.6×10-15kg,带电量为q=1.6×10-7C的带电粒子,从坐标原点O以v0=5.0×105m/s的速度沿与x轴成30°角的方向斜向上射出,经磁场偏转恰好从x轴上的Q点飞过,经过Q点时的速度方向也斜向上(不计重力,π=3.14,计算结果保留3位有效数字),求:
如图所示xoy平面内,y≥5cm和y<0的范围内存在匀强磁场,磁场方向垂直纸面向里,磁感应强度均为B=1.0T,一个质量为m=1.6×10-15kg,带电量为q=1.6×10-7C的带电粒子,从坐标原点O以v0=5.0×105m/s的速度沿与x轴成30°角的方向斜向上射出,经磁场偏转恰好从x轴上的Q点飞过,经过Q点时的速度方向也斜向上(不计重力,π=3.14,计算结果保留3位有效数字),求:(1)粒子从O到运动到Q所用的最短时间;
(2)粒子从O到运动到Q点的所通过的路程.
分析 (1)粒子在磁场中做匀速圆周运动,在没有磁场的区域中做匀速直线运动,粒子经历的周期数越少,则粒子运动的时间越短;
(2)粒子的运动情况可以不断的重复上述情况,粒子的路程为在磁场中的路程与在没有磁场的区域中的路程的和.
解答 解:(1)粒子的运动轨迹如图所示
当粒子第一次以斜向上的速度经过Q点时,时间最短;在磁场中运动时间为t1,有:$q{v}_{0}B=\frac{m{v}_{0}^{2}}{r}$
得:$r=\frac{m{v}_{0}}{qB}$
又:$T=\frac{2πr}{v}=\frac{2πm}{qB}$
代入数据得:r=0.05m,T=6.28×10-7s
由图可知,粒子在磁场中运动的时间是一个周期,所以:
${t}_{1}=T=6.28×1{0}^{-7}$s
在无场区域运动的时间为t2,有:${t}_{2}=\frac{4d}{v}=\frac{4×0.05}{5.0×1{0}^{-5}}s=4.0×1{0}^{-7}$s
$t={t}_{1}+{t}_{2}=1.028×1{0}^{-6}$s
(2)粒子的运动情况可以不断的重复上述情况,粒子在磁场中的路程为:
s1=2n•πr(n=1,2,3…)
在无场区的路程为:s2=4nd(n=1,2,3…)
总路程为:s=s1+s2=0.514n(n=1,2,3…) 
答:(1)粒子从O到运动到Q所用的最短时间是1.028×10-6s;
(2)粒子从O到运动到Q点的所通过的路程是0.514n,(n=1,2,3…)
点评 本题考查了粒子在磁场中的运动,分析清楚粒子的运动过程,应用牛顿第二定律、粒子周期公式即可正确解题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
2. 如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
 如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )
如图所示,理想变压器原线圈通过理想电流表接在输出电压u=220$\sqrt{2}$sin100πtV的交流电源的两端,副线圈中接有理想电压表及阻值R=50Ω的负载电阻,已知原、副线圈匝数之比为11:1,则下列说法中正确的是( )| A. | 电流表的示数为4.4A | |
| B. | 原线圈的输入功率为16W | |
| C. | 电压表的示数为20V | |
| D. | 通过电阻R的交变电流的频率为100Hz |
9.下列说法正确的是( )
| A. | 胡克通过实验研究,发现了弹簧弹力所遵循的规律 | |
| B. | 伽利略是动力学的奠基人,他总结和发展了前人的成果,发现了力和运动的关系 | |
| C. | 牛顿巧妙地运用科学的推理,通过斜面实验,推断出力不是维持物体运动状态的原因 | |
| D. | 库仑巧妙的利用“库仑扭秤”研究电荷之间的作用,发现了“库仑定律” |
6.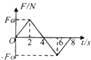 一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )
一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )
 一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )
一质点在某一外力F作用下由静止开始运动,力F的大小随时间t变化的图象如图所示,其方向始终在一条直线上,在0-8s内,下列说法正确的是( )| A. | 在0-2s内质点做匀加速运动,第2s末其速度达到最大值 | |
| B. | 第4s末质点的加速度为零,速度也刚好为零 | |
| C. | 质点做变加速直线运动,第6s末加速度最大,且离出发位置最远 | |
| D. | 在0-8s内,质点一直向同一个方向做直线运动,在第8s末速度和加速度都为零,且离出发点最远 |
4.若规定向正东为位移的正方向,今有一个皮球停在水平面的某处,轻踢它一脚,使它向正东做直线运动,运动5m远与墙相碰,后又向正西做直线运动,运动7m后停下.则上述过程中皮球通过的路程和位移分别是( )
| A. | 12m、2m | B. | 12m、-2m | C. | -2m、2m | D. | 2m、-2m |
 滑板运动是青少年喜爱的一项活动.如图所示,滑板运动员以某一初速度从A点水平离开h=0.8m高的平台,运动员(连同滑板)恰好能无碰撞的从B点沿圆弧切线进入竖直光滑圆弧轨道,然后经C点沿固定斜面向上运动至最高点D,B、C为圆弧的两端点,其连线水平,轨道半径R=1.0m,圆弧对应圆心角θ=106°,E为圆弧的最低点,斜面与圆弧相切于C点.已知滑板与斜面间的动摩擦因数为μ=$\frac{1}{3}$,g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,运动员(连同滑板),可视为质点,其质量m=1kg.求:
滑板运动是青少年喜爱的一项活动.如图所示,滑板运动员以某一初速度从A点水平离开h=0.8m高的平台,运动员(连同滑板)恰好能无碰撞的从B点沿圆弧切线进入竖直光滑圆弧轨道,然后经C点沿固定斜面向上运动至最高点D,B、C为圆弧的两端点,其连线水平,轨道半径R=1.0m,圆弧对应圆心角θ=106°,E为圆弧的最低点,斜面与圆弧相切于C点.已知滑板与斜面间的动摩擦因数为μ=$\frac{1}{3}$,g=10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力,运动员(连同滑板),可视为质点,其质量m=1kg.求: 如图所示.在oxy平面第一象限的OP直线上方.有场强大小为E、沿y轴负方向的匀强电场,在OP直线和OQ盧线的下方,有垂直纸面向外的匀强磁场.在y轴上的a点,将质量为m、电荷最为+q的带电微粒以速度v0水平射入电场,经过一段时间后带电粒子从c点以一定的速度垂直于OP直线进入匀强磁场,当粒子经过X轴时速度方向与X轴垂直,再经过一段时间,带电粒子到达y轴上的b点.试求带电粒从a点开始运动到b点所用的时间(已知a=37°,θ=53°,sin37°=0.6,sin53°=0.8.带电微粒的重力不计).
如图所示.在oxy平面第一象限的OP直线上方.有场强大小为E、沿y轴负方向的匀强电场,在OP直线和OQ盧线的下方,有垂直纸面向外的匀强磁场.在y轴上的a点,将质量为m、电荷最为+q的带电微粒以速度v0水平射入电场,经过一段时间后带电粒子从c点以一定的速度垂直于OP直线进入匀强磁场,当粒子经过X轴时速度方向与X轴垂直,再经过一段时间,带电粒子到达y轴上的b点.试求带电粒从a点开始运动到b点所用的时间(已知a=37°,θ=53°,sin37°=0.6,sin53°=0.8.带电微粒的重力不计).
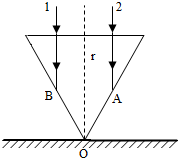 在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合,已知玻璃的折射率为n=$\sqrt{3}$,则:
在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示,有一半径为r的圆柱形平行光束垂直入射到圆锥的底面上,光束的中心轴与圆锥的轴重合,已知玻璃的折射率为n=$\sqrt{3}$,则: