题目内容
14．A、B是一条电场线上的两点，如图所示，正电荷从A移动到B，电场力做正功．请画出这条电场线的方向，并回答：①A、B中哪点电势高？②负电荷从A移动到B，电势能是增加还是减小？
分析 电场力做正功时，电场力方向与位移方向相同．电场力方向与位移方向相反时，电场力做负功．确定出电场力方向，即可分析电场线的方向，从而判断出电势的高低．
解答 
解：正电荷从A移动到B，电场力做正功，说明正电荷受到的电场力由A指向B，则电场线方向向右．如图．
①根据顺着电场线方向电势降低，可知A点的电势高．
②负电荷从A移动到B，电场力做负功，电势能增加．
答：画出这条电场线的方向如图．①A、B中A点电势高．②负电荷从A移动到B，电势能是增加．
点评 判断电场力做功正负的关键是看电场力的方向与位移方向的夹角，与力中判断方法一样．要知道正电荷电场力与场强同向，负电荷电场力与场强反向．
练习册系列答案
相关题目
4．假设某暗物质粒子质量为m，速度为v，则其动能大小为（ ）
| A． | mv | B． | $\frac{1}{2}$mv | C． | mv2 | D． | $\frac{1}{2}$mv2 |
5．
如图是滑雪场的一条雪道．质量为70kg的某滑雪运动员由A点沿圆弧轨道滑下，在B点以5$\sqrt{3}$m/s的速度水平飞出，落到了倾斜轨道上的C点（图中未画出）．不计空气阻力，θ=30°，g=10m/s2，则下列判断正确的是（ ）
如图是滑雪场的一条雪道．质量为70kg的某滑雪运动员由A点沿圆弧轨道滑下，在B点以5$\sqrt{3}$m/s的速度水平飞出，落到了倾斜轨道上的C点（图中未画出）．不计空气阻力，θ=30°，g=10m/s2，则下列判断正确的是（ ）| A． | 该滑雪运动员腾空的时间为1s | |
| B． | BC两点间的落差为5$\sqrt{3}$m | |
| C． | 落到C点时重力的瞬时功率为3500$\sqrt{7}$W | |
| D． | 若该滑雪运动员从更高处滑下，落到C点时速度与竖直方向的夹角变小 |
2．
已知通电长直导线周围某点的磁感应强度B=k$\frac{I}{r}$，即磁感应强度B与导线中的电流I成正比、与该点到导线的距离r成反比．如图，两根互相平行的长直导线过纸面上的M、N两点，且与纸面垂直，导线中通有大小相等、方向相同的电流．a、o、b在M、N的连线上，o为MN的中点，c、d位于MN的中垂线上，且a、b、c、d到o点的距离均相等．关于以上几点处的磁场，下列说法正确的是（ ）
已知通电长直导线周围某点的磁感应强度B=k$\frac{I}{r}$，即磁感应强度B与导线中的电流I成正比、与该点到导线的距离r成反比．如图，两根互相平行的长直导线过纸面上的M、N两点，且与纸面垂直，导线中通有大小相等、方向相同的电流．a、o、b在M、N的连线上，o为MN的中点，c、d位于MN的中垂线上，且a、b、c、d到o点的距离均相等．关于以上几点处的磁场，下列说法正确的是（ ）| A． | o点处的磁感应强度最大 | |
| B． | a、b两点处的磁感应强度大小相等，方向相反 | |
| C． | c、d两点处的磁感应强度大小相等，方向相同 | |
| D． | a、b、c、d四点处磁感应强度的大小相等，方向不同 |
9．
某交流发电机的输出电压随时间变化的图象如图所示，输出功率是50kW，现用5000V高压输电，输电线上的总电阻是50Ω，再利用n1：n2=20：1的降压变压器降压后供给用户，则下列说法正确的是（ ）
某交流发电机的输出电压随时间变化的图象如图所示，输出功率是50kW，现用5000V高压输电，输电线上的总电阻是50Ω，再利用n1：n2=20：1的降压变压器降压后供给用户，则下列说法正确的是（ ）| A． | 发电机输出电压的有效值为220$\sqrt{2}$V | |
| B． | 若输电线两端的电压提高到原来的4倍，输电线上损失的功率为原来的$\frac{1}{4}$ | |
| C． | 输电功率为80% | |
| D． | 降压变压器输出电压的有效值为225V，交变电流的频率为50Hz |
6．
如图所示，一质量为m的金属杆可以无摩擦地沿水平的平行导轨滑行，两轨间宽为L，导轨与电阻R连接，放在竖直向的匀强磁场中，磁场的磁感应强度为B，杆的初速度为v，其余电阻不计，则（ ）
如图所示，一质量为m的金属杆可以无摩擦地沿水平的平行导轨滑行，两轨间宽为L，导轨与电阻R连接，放在竖直向的匀强磁场中，磁场的磁感应强度为B，杆的初速度为v，其余电阻不计，则（ ）| A． | 由于金属杆和导轨之间无摩擦力，回路中的感应电动势始终是BLv | |
| B． | 金属杆所受的安培力方向与初速度方向相反 | |
| C． | 金属杆所受的安培力逐渐增大 | |
| D． | 电阻R上产生的总焦耳热为$\frac{1}{2}$mv2 |
15．
如图所示，竖直固定放置的粗糙斜面AB的下端与光滑的圆弧轨道BCD的B端相切，圆弧轨道的半径为R，圆心O与A、D在同一水平面上，∠COB=θ=45°，现使一质量为m的小物体从D点无初速滑下，小物块与粗糙斜面AB间的动摩擦因数为μ＜tanθ，则关于小物块的运动情况，下列说法正确的是（ ）
如图所示，竖直固定放置的粗糙斜面AB的下端与光滑的圆弧轨道BCD的B端相切，圆弧轨道的半径为R，圆心O与A、D在同一水平面上，∠COB=θ=45°，现使一质量为m的小物体从D点无初速滑下，小物块与粗糙斜面AB间的动摩擦因数为μ＜tanθ，则关于小物块的运动情况，下列说法正确的是（ ）| A． | 小物块可能运动到A点 | |
| B． | 小物块最终将停在C点 | |
| C． | 小物块通过圆弧轨道最低点C时，对C点的最大压力为3mg | |
| D． | 小物块通过圆弧轨道最低点C时，对C点的最大压力为（3-$\sqrt{2}$μ）mg |
16．
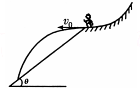如图所示，在高台滑雪比赛中，某运动员从平台上以v0的初速度沿水平方向飞出后，落到倾角为θ的雪坡上（雪坡足够长）．若运动员可视为质点，不计空气阻力，重力加速度为g，则（ ）
如图所示，在高台滑雪比赛中，某运动员从平台上以v0的初速度沿水平方向飞出后，落到倾角为θ的雪坡上（雪坡足够长）．若运动员可视为质点，不计空气阻力，重力加速度为g，则（ ）| A． | 如果v0不同，运动员落到雪坡时的位置不同，速度方向也不同 | |
| B． | 如果v0不同，运动员落到雪坡时的位置不同，但空中运动时间相同 | |
| C． | 运动员刚要落到雪坡上时的速度大小为$\frac{{v}_{0}}{cosθ}$ | |
| D． | 运动员在空中经历的时间为$\frac{2{v}_{0}tanθ}{g}$ |