��Ŀ����
13��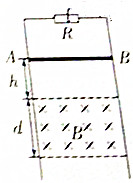 ��ͼ��ʾ���������費�ơ����ΪL�Ĺ⻬����������ֱ���ã������϶˽ӵ���R��һ����Ϊm������Ϊr�ĵ����AB��ֱ���ڵ����ϣ��ھ�AB���·�h���������������������ڷֲ��дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ����ƽ���������Ϊd����ʹ��AB�ɾ�ֹ��ʼ�ͷţ��ڰ�AB�뿪�ų�ǰ�Ѿ�������ֱ���˶��������������ʼ�ձ���ˮƽ�����뵼��Ӵ����ã���֪�������ٶ�Ϊg�����AB��ͨ���ų�����Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ���������費�ơ����ΪL�Ĺ⻬����������ֱ���ã������϶˽ӵ���R��һ����Ϊm������Ϊr�ĵ����AB��ֱ���ڵ����ϣ��ھ�AB���·�h���������������������ڷֲ��дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ����ƽ���������Ϊd����ʹ��AB�ɾ�ֹ��ʼ�ͷţ��ڰ�AB�뿪�ų�ǰ�Ѿ�������ֱ���˶��������������ʼ�ձ���ˮƽ�����뵼��Ӵ����ã���֪�������ٶ�Ϊg�����AB��ͨ���ų�����Ĺ����У�����˵����ȷ���ǣ�������| A�� | ͨ��R�ĵ����Ϊq=$\frac{BLd}{R+r}$ | |
| B�� | �뿪�ų�˲�䣬��AB���ٶȴ�СΪv=$\frac{mg��R+r��}{{B}^{2}{L}^{2}}$ | |
| C�� | �ù����а����������Ĺ�ΪW=mg��h+d��-$\frac{{m}^{2}{g}^{2}��R+r��^{2}}{2{B}^{2}{L}^{2}}$ | |
| D�� | ��h��$\frac{{m}^{2}g��R+r��^{2}}{2{B}^{4}{L}^{4}}$ʱ��������ų����ȼ��ٺ����� |
���� ����q=$\frac{����}{R+r}$��ͨ��R�ĵ��������AB���뿪�ų�ǰ�Ѿ�������ֱ���˶�������ƽ��״̬���ɰ�������ʽ��ƽ����������������뿪�ų�ʱ���ٶȣ���AB����ʼ�»������뿪�ų��Ĺ��̣����ö��ܶ���������������������Ĺ������ݰ�����ų�ʱ���ٶȴ�С���������ڴų��е��˶������
��� �⣺A��ͨ��R�ĵ����Ϊ q=$\frac{����}{R+r}$=$\frac{BLd}{R+r}$����A��ȷ��
B��MN���뿪�ų��߽�ǰ�������˶������ٶ�Ϊv����������ĵ綯��Ϊ E=BLv
��·�е��� I=$\frac{E}{R+r}$
��AB������ƽ�������� mg-BIL=0
��� v=$\frac{mg��R+r��}{{B}^{2}{L}^{2}}$����B��ȷ��
C����AB����ʼ�»������뿪�ų��Ĺ��̣����ö��ܶ�����
mg��h+d��-W=$\frac{1}{2}m{v}^{2}$
��� W=mg��h+d��-$\frac{{m}^{3}{g}^{2}��R+r��^{2}}{{B}^{4}{L}^{4}}$����C����
D����������Ϳ�ʼ�������˶������ʱ h=$\frac{{v}^{2}}{2g}$=$\frac{{m}^{2}g��R+r��^{2}}{2{B}^{4}{L}^{4}}$
��h��$\frac{{m}^{2}g��R+r��^{2}}{2{B}^{4}{L}^{4}}$ʱ��������ų�ʱ�������ڰ������������������˶�����D����
��ѡ��AB
���� ����Ҫ���ո�Ӧ�������ʽq=$\frac{����}{R+r}$��Ҫ���Ƶ��������ı���ʽ��ͬʱҪ��ȷ�������������ת���ģ��������������Ƕ��о���Ÿ�Ӧ����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� ��ͼ��ʾ��A��BΪƽ�а�������Ľ����壬GΪ����ƣ���ʼʱ����S�պϣ������ָ���ſ�һ���Ƕȣ����в�����ʹָ���ſ��Ƕ�����һЩ���ǣ�������
��ͼ��ʾ��A��BΪƽ�а�������Ľ����壬GΪ����ƣ���ʼʱ����S�պϣ������ָ���ſ�һ���Ƕȣ����в�����ʹָ���ſ��Ƕ�����һЩ���ǣ�������| A�� | ���ֿ���S�պϣ���R�ϵĻ�Ƭ�����ƶ� | |
| B�� | ���ֿ���S�պϣ���A��B������ֿ�һЩ | |
| C�� | �Ͽ�����S��A��B����������������СһЩ | |
| D�� | �Ͽ�����S��A��B������ֿ�һЩ |
| A�� | ����ij��ٶ���10 m/s | B�� | ����ļ��ٶ���-4 m/s | ||
| C�� | ����ļ��ٶ���8 m/s2 | D�� | ������2 sĩ���ٶ�Ϊ-6 m/s |
 ��ͼ��ʾ������ΪM�ij�ľ�徲ֹ�ڹ⻬��ˮƽ���ϣ�����Ϊm��ľ���Գ��ٶ�v0��������ˮƽ���ϳ�ľ�壮��֪ľ����ľ���Ķ�Ħ������Ϊ�̣���ľ���ڳ�ľ���ϻ����Ĺ����У���ľ��ļ��ٶȴ�СΪ��������
��ͼ��ʾ������ΪM�ij�ľ�徲ֹ�ڹ⻬��ˮƽ���ϣ�����Ϊm��ľ���Գ��ٶ�v0��������ˮƽ���ϳ�ľ�壮��֪ľ����ľ���Ķ�Ħ������Ϊ�̣���ľ���ڳ�ľ���ϻ����Ĺ����У���ľ��ļ��ٶȴ�СΪ��������| A�� | 0 | B�� | ��g | C�� | $\frac{��Mg}{m}$ | D�� | $\frac{��mg}{M}$ |
 �뾶ΪR�Ĺ̶���Բ�β���ש�ĺ������ͼ��ʾ��O��ΪԲ�ģ�OO����ֱ��AB��ֱ���㹻��Ĺ���CD�����ڲ���ש���������AB��ֱ��һ�����ذ뾶������OO��ɦ�=30������O�㣬����CD�������������ߣ���֪������������Ϊ$\sqrt{2}$����
�뾶ΪR�Ĺ̶���Բ�β���ש�ĺ������ͼ��ʾ��O��ΪԲ�ģ�OO����ֱ��AB��ֱ���㹻��Ĺ���CD�����ڲ���ש���������AB��ֱ��һ�����ذ뾶������OO��ɦ�=30������O�㣬����CD�������������ߣ���֪������������Ϊ$\sqrt{2}$���� ijͬѧ�о���ײ���⣬�������ͼ��ʾ��װ�ã��컨�����õȳ���ϸ����ֱ����������С�����С���Ժ��ԣ�ϸ�߳���ΪR��A������Ϊm��B������ΪM������M=3m���������ٶ�Ϊg���ֽ�A������ˮƽλ�ã�����ϸ����ֱ������������ͼ������ʾ������A������ֱ���µij��ٶȣ�ʹA��B��������͵㷢����������������A��պ��ܵ��س�ʼ��ˮƽλ�ã���
ijͬѧ�о���ײ���⣬�������ͼ��ʾ��װ�ã��컨�����õȳ���ϸ����ֱ����������С�����С���Ժ��ԣ�ϸ�߳���ΪR��A������Ϊm��B������ΪM������M=3m���������ٶ�Ϊg���ֽ�A������ˮƽλ�ã�����ϸ����ֱ������������ͼ������ʾ������A������ֱ���µij��ٶȣ�ʹA��B��������͵㷢����������������A��պ��ܵ��س�ʼ��ˮƽλ�ã���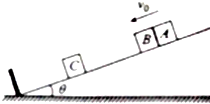 ��ͼ��ʾ�����Ϊ��=30���б��̶���ˮƽ���ϣ�б�����һ������֮��ֱ��ͬ�ֲ����ƳɵĿɿ�Ϊ�ʵ��С���A��B��C���������ֱ�Ϊm��2m��2m�����C��ֹ�����B�뵲��֮��ijһλ�ã�С���A��B����һ������������ըҩ��һ����v0=4m/s���ٶ���б�������»�����A��B�뵲�����ΪL=1.75mʱըҩ��ը��ըҩ��ը��A���ٶ�ǡ�ñ�Ϊ�㣬���С���B��б�������˶�����С���C����������ײ���������C�뵲��Ҳ����������ײ���������C��б���ϻ���������B��A��ײ��ճ��һ�壮ȡg=10m/s2�������B��A����ײ����ٶȴ�Сv����
��ͼ��ʾ�����Ϊ��=30���б��̶���ˮƽ���ϣ�б�����һ������֮��ֱ��ͬ�ֲ����ƳɵĿɿ�Ϊ�ʵ��С���A��B��C���������ֱ�Ϊm��2m��2m�����C��ֹ�����B�뵲��֮��ijһλ�ã�С���A��B����һ������������ըҩ��һ����v0=4m/s���ٶ���б�������»�����A��B�뵲�����ΪL=1.75mʱըҩ��ը��ըҩ��ը��A���ٶ�ǡ�ñ�Ϊ�㣬���С���B��б�������˶�����С���C����������ײ���������C�뵲��Ҳ����������ײ���������C��б���ϻ���������B��A��ײ��ճ��һ�壮ȡg=10m/s2�������B��A����ײ����ٶȴ�Сv����