题目内容
1.在发射载人宇宙飞船向上加速过程中,宇航员处于超重(填“超重”或“失重”)状态;在返回舱减速降落至地面过程中,宇航员处于超重(填“超重”或“失重”)状态.分析 当物体对接触面的压力大于物体的真实重力时,就说物体处于超重状态,此时有向上的加速度;
当物体对接触面的压力小于物体的真实重力时,就说物体处于失重状态,此时有向下的加速度;
如果没有压力了,那么就是处于完全失重状态,此时向下加速度的大小为重力加速度g.
解答 解:在飞船发射过程中向上加速时,加速度方向向上,处于超重状态.在降落过程中减速时,加速度方向向上,处于超重状态.
故答案为:超重 超重
点评 解决本题的关键知道超重和失重的运动学特征,同时要注意超重和失重时,重力没有变化.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
6.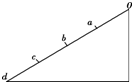 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 在斜面上运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |
13.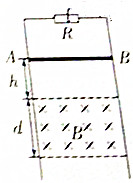 如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )
如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )
 如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )
如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )| A. | 通过R的电荷量为q=$\frac{BLd}{R+r}$ | |
| B. | 离开磁场瞬间,棒AB的速度大小为v=$\frac{mg(R+r)}{{B}^{2}{L}^{2}}$ | |
| C. | 该过程中安培力所做的功为W=mg(h+d)-$\frac{{m}^{2}{g}^{2}(R+r)^{2}}{2{B}^{2}{L}^{2}}$ | |
| D. | 当h<$\frac{{m}^{2}g(R+r)^{2}}{2{B}^{4}{L}^{4}}$时,棒进入磁场后先减速后匀速 |
7. 如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
 如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )| A. | 电场线与ac直线平行 | B. | 电场方向与ac直线垂直 | ||
| C. | b点电势为3V | D. | b、d位于同一等势面上 |
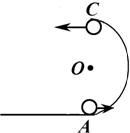 如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m.质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点、与圆心O等高点、最高点.小球过这三点的速度分别为vA=5m/s,vB=4m∠s,vC=3m/s,求:
如图所示,竖直的半圆形轨道与水平面相切,轨道半径R=0.2m.质量m=200g的小球以某一速度正对半圆形轨道运动,A、B、C三点分别为圆轨道最低点、与圆心O等高点、最高点.小球过这三点的速度分别为vA=5m/s,vB=4m∠s,vC=3m/s,求: 如图,三角形AOB为等腰直角三棱镜的横截面,以OA、OB为轴建立直角坐标系xoy,OA=OB=L,棱镜的折射率为n=$\sqrt{2}$.一束平行于斜边AB的平行光从OB边射入.光透过棱镜只考虑一次内部反射.
如图,三角形AOB为等腰直角三棱镜的横截面,以OA、OB为轴建立直角坐标系xoy,OA=OB=L,棱镜的折射率为n=$\sqrt{2}$.一束平行于斜边AB的平行光从OB边射入.光透过棱镜只考虑一次内部反射. 如图所示,匀强磁场垂直于矩形线框abcd,磁场的磁感应强度为B,矩形面积为S.现使矩形框以ab边为轴转动90°角,则在这个过程中,穿过线框的磁通量变化量的数值是BS.
如图所示,匀强磁场垂直于矩形线框abcd,磁场的磁感应强度为B,矩形面积为S.现使矩形框以ab边为轴转动90°角,则在这个过程中,穿过线框的磁通量变化量的数值是BS. n=100匝的圆形线圈,处在如图所示的磁场内(线圈右边的电路中没有磁场),磁场均匀增大,线圈磁通量的变化率$\frac{△φ}{△t}$=0.004 Wb/s,线圈电阻r=1Ω,R=3Ω,求:
n=100匝的圆形线圈,处在如图所示的磁场内(线圈右边的电路中没有磁场),磁场均匀增大,线圈磁通量的变化率$\frac{△φ}{△t}$=0.004 Wb/s,线圈电阻r=1Ω,R=3Ω,求: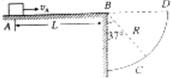 如图所示,水平面AB的右侧有一圆形挡板,圆的半径R=0.16m,B为圆心,BC连线与竖直方向的夹角为37°,可视为质点的滑块以一定的初速度从水平面上的A点沿AB方向运动,恰好落在圆形挡板的C点.已知AB间距为L=2.16m,滑块与水平面间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6.求:
如图所示,水平面AB的右侧有一圆形挡板,圆的半径R=0.16m,B为圆心,BC连线与竖直方向的夹角为37°,可视为质点的滑块以一定的初速度从水平面上的A点沿AB方向运动,恰好落在圆形挡板的C点.已知AB间距为L=2.16m,滑块与水平面间的动摩擦因数μ=0.2,取g=10m/s2,sin37°=0.6.求: