题目内容
2．
如图所示，质量为M的长木板静止于光滑的水平面上，质量为m的木块以初速度v0从左向右水平滑上长木板．已知木块与木板间的动摩擦因数为μ，则木块在长木板上滑动的过程中，长木板的加速度大小为（ ）| A． | 0 | B． | μg | C． | $\frac{μMg}{m}$ | D． | $\frac{μmg}{M}$ |
分析 根据滑动摩擦力公式可求得两物体间的摩擦力；再分析木板的受力情况，根据力的合成求出合力，再根据牛顿第二定律求出木板的加速度．
解答 解：对M进行受力分析可知，M水平方向受到m对M的滑动摩擦力，方向水平向右，摩擦力大小f=μmg；
根据牛顿第二定律得：
a=$\frac{f}{M}$=$\frac{μmg}{M}$
加速度的方向水平向右
故选：D．
点评 本题考查牛顿第二定律的应用问题，要注意正确选择研究对象，并能确定两物体之间的联系，正确受力分析，再根据牛顿第二定律求解．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
n=100匝的圆形线圈，处在如图所示的磁场内（线圈右边的电路中没有磁场），磁场均匀增大，线圈磁通量的变化率$\frac{△φ}{△t}$=0.004 Wb/s，线圈电阻r=1Ω，R=3Ω，求：
13．
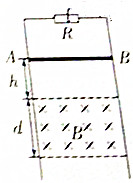如图所示，两根电阻不计、间距为L的光滑金属导轨竖直放置，导轨上端接电阻R，一质量为m，电阻为r的导体棒AB垂直放在导轨上，在距AB棒下方h处，在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场，磁场方向垂直导轨平面向里，宽度为d，现使棒AB由静止开始释放，在棒AB离开磁场前已经做匀速直线运动，棒下落过程中始终保持水平，并与导轨接触良好，已知重力加速度为g，则棒AB在通过磁场区域的过程中，下列说法正确的是（ ）
如图所示，两根电阻不计、间距为L的光滑金属导轨竖直放置，导轨上端接电阻R，一质量为m，电阻为r的导体棒AB垂直放在导轨上，在距AB棒下方h处，在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场，磁场方向垂直导轨平面向里，宽度为d，现使棒AB由静止开始释放，在棒AB离开磁场前已经做匀速直线运动，棒下落过程中始终保持水平，并与导轨接触良好，已知重力加速度为g，则棒AB在通过磁场区域的过程中，下列说法正确的是（ ）| A． | 通过R的电荷量为q=$\frac{BLd}{R+r}$ | |
| B． | 离开磁场瞬间，棒AB的速度大小为v=$\frac{mg（R+r）}{{B}^{2}{L}^{2}}$ | |
| C． | 该过程中安培力所做的功为W=mg（h+d）-$\frac{{m}^{2}{g}^{2}（R+r）^{2}}{2{B}^{2}{L}^{2}}$ | |
| D． | 当h＜$\frac{{m}^{2}g（R+r）^{2}}{2{B}^{4}{L}^{4}}$时，棒进入磁场后先减速后匀速 |
20．电梯经过启动、匀速运行和制动三个过程，从低楼层到达高楼层，启动和制动可看作是匀变速直线运动．电梯竖直向上运动过程中速度的变化情况如下表：
则前5秒内电梯通过的位移大小为18.75m．
| 时间（s） | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 速度（m/s） | 0 | 2.0 | 4.0 | 5.0 | 5.0 | 5.0 | 5.0 | 5.0 | 4.0 | 3.0 | 2.0 | 1.0 | 0 |
7．
如图所示，匀强电场中有a、b、c、d四点，四点刚好构成一个矩形，已知∠acd=30°，电场方向与矩形所在平面平行，已知a、d和c点的电势分别为（4-$\sqrt{3}$）V、4V和（4+$\sqrt{3}$）V，则（ ）
如图所示，匀强电场中有a、b、c、d四点，四点刚好构成一个矩形，已知∠acd=30°，电场方向与矩形所在平面平行，已知a、d和c点的电势分别为（4-$\sqrt{3}$）V、4V和（4+$\sqrt{3}$）V，则（ ）| A． | 电场线与ac直线平行 | B． | 电场方向与ac直线垂直 | ||
| C． | b点电势为3V | D． | b、d位于同一等势面上 |
关于在做“验证力的平行四边形定则”实验时：
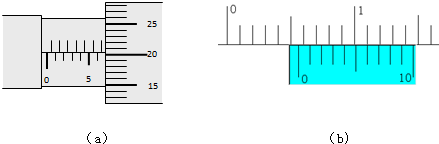
某实验小组用下图实验装置验证力的平行四边形定则，实验时将坐标纸固定在竖直放置的木板上，先将弹簧秤A一端的细绳固定在木板上的P点，另一端通过细绳把弹簧秤B、重物系在一点，实验时水平牵引弹簧秤B使重物静止，记录完需要的数据和内容后，重物挂在弹簧秤A下端保持静止并记录，然后根据记录的数据和内容在坐标纸上验证力的平行四边形定则．