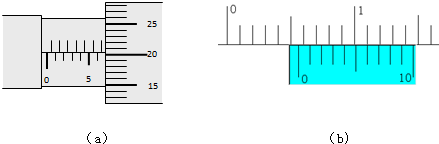
��Ŀ����
4�� �뾶ΪR�Ĺ̶���Բ�β���ש�ĺ������ͼ��ʾ��O��ΪԲ�ģ�OO����ֱ��AB��ֱ���㹻��Ĺ���CD�����ڲ���ש���������AB��ֱ��һ�����ذ뾶������OO��ɦ�=30������O�㣬����CD�������������ߣ���֪������������Ϊ$\sqrt{2}$����
�뾶ΪR�Ĺ̶���Բ�β���ש�ĺ������ͼ��ʾ��O��ΪԲ�ģ�OO����ֱ��AB��ֱ���㹻��Ĺ���CD�����ڲ���ש���������AB��ֱ��һ�����ذ뾶������OO��ɦ�=30������O�㣬����CD�������������ߣ���֪������������Ϊ$\sqrt{2}$������1�����ȱ�Ϊ���ʱ�������ǡ�ñ�Ϊһ����
��2���������ذ뾶������OO��ɦ�=30������O��ʱ������CD����������ߵľ��룮
���� ��1������������ڹ�ķ��������ֱ��γɵģ��������������ǡ�ñ�Ϊһ��ʱ������ǡ����AB��ǡ�÷�����ȫ���䣮�����ٽ�ǹ�ʽ��⣮
��2���������ذ뾶������OO��ɦ�=30������O��ʱ��������ABͬʱ������������䣬��������ذ뾶�����P�㣬�ɼ���֪ʶ���AP�ij��ȣ�������䶨����⣮
���  �⣺��1�������ϵ��������ǡ�ñ�Ϊһ��ʱ������ǡ����AB��ǡ�÷�����ȫ���䣮���У�
�⣺��1�������ϵ��������ǡ�ñ�Ϊһ��ʱ������ǡ����AB��ǡ�÷�����ȫ���䣮���У�
n=$\frac{1}{sin��}$
����=45��
��2���������ذ뾶������OO��ɦ�=30������O��ʱ��������ABͬʱ������������䣬��������ذ뾶�����P�㣬��=��=30��
�ɵã�AP=Rcot��=$\sqrt{3}$R
��AB�������䣬��n=$\frac{sin��}{sin30��}$
��ã�sin��=$\frac{\sqrt{2}}{2}$����=45��
�ɵ� AQ=R
�������ľ���Ϊ��PQ=AP+AQ=��$\sqrt{3}$+1��R
�𣺣�1�����ȱ�Ϊ45��ʱ�������ǡ�ñ�Ϊһ����
��2���������ذ뾶������OO��ɦ�=30������O��ʱ������CD����������ߵľ����ǣ�$\sqrt{3}$+1��R��
���� ���ڼ��ι�ѧ���⣬�ؼ�Ҫ��ȷ������·ͼ���������䶨�ɺͼ���֪ʶ��Ͻ��д�����

��ϰ��ϵ�д�
 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
�����Ŀ
14�� M��NΪ�������߹ܣ����ǵ�������ͼ��ʾ��c��d��e��f�ֱ�ΪM��N��������������a��b�ֱ�Ϊ��Դ��������������������ʹ��ͨ�����߹ܼ���������Ϊ������������
M��NΪ�������߹ܣ����ǵ�������ͼ��ʾ��c��d��e��f�ֱ�ΪM��N��������������a��b�ֱ�Ϊ��Դ��������������������ʹ��ͨ�����߹ܼ���������Ϊ������������
 M��NΪ�������߹ܣ����ǵ�������ͼ��ʾ��c��d��e��f�ֱ�ΪM��N��������������a��b�ֱ�Ϊ��Դ��������������������ʹ��ͨ�����߹ܼ���������Ϊ������������
M��NΪ�������߹ܣ����ǵ�������ͼ��ʾ��c��d��e��f�ֱ�ΪM��N��������������a��b�ֱ�Ϊ��Դ��������������������ʹ��ͨ�����߹ܼ���������Ϊ������������| A�� | a��c��b��f��d��e������ | B�� | a��d��b��f��c��e������ | ||
| C�� | a��c��b��e��d��f������ | D�� | a��d��b��e��c��f������ |
13��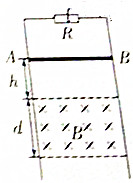 ��ͼ��ʾ���������費�ơ����ΪL�Ĺ⻬����������ֱ���ã������϶˽ӵ���R��һ����Ϊm������Ϊr�ĵ����AB��ֱ���ڵ����ϣ��ھ�AB���·�h���������������������ڷֲ��дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ����ƽ���������Ϊd����ʹ��AB�ɾ�ֹ��ʼ�ͷţ��ڰ�AB�뿪�ų�ǰ�Ѿ�������ֱ���˶��������������ʼ�ձ���ˮƽ�����뵼��Ӵ����ã���֪�������ٶ�Ϊg�����AB��ͨ���ų�����Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ���������費�ơ����ΪL�Ĺ⻬����������ֱ���ã������϶˽ӵ���R��һ����Ϊm������Ϊr�ĵ����AB��ֱ���ڵ����ϣ��ھ�AB���·�h���������������������ڷֲ��дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ����ƽ���������Ϊd����ʹ��AB�ɾ�ֹ��ʼ�ͷţ��ڰ�AB�뿪�ų�ǰ�Ѿ�������ֱ���˶��������������ʼ�ձ���ˮƽ�����뵼��Ӵ����ã���֪�������ٶ�Ϊg�����AB��ͨ���ų�����Ĺ����У�����˵����ȷ���ǣ�������
 ��ͼ��ʾ���������費�ơ����ΪL�Ĺ⻬����������ֱ���ã������϶˽ӵ���R��һ����Ϊm������Ϊr�ĵ����AB��ֱ���ڵ����ϣ��ھ�AB���·�h���������������������ڷֲ��дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ����ƽ���������Ϊd����ʹ��AB�ɾ�ֹ��ʼ�ͷţ��ڰ�AB�뿪�ų�ǰ�Ѿ�������ֱ���˶��������������ʼ�ձ���ˮƽ�����뵼��Ӵ����ã���֪�������ٶ�Ϊg�����AB��ͨ���ų�����Ĺ����У�����˵����ȷ���ǣ�������
��ͼ��ʾ���������費�ơ����ΪL�Ĺ⻬����������ֱ���ã������϶˽ӵ���R��һ����Ϊm������Ϊr�ĵ����AB��ֱ���ڵ����ϣ��ھ�AB���·�h���������������������ڷֲ��дŸ�Ӧǿ��ΪB����ǿ�ų����ų�����ֱ����ƽ���������Ϊd����ʹ��AB�ɾ�ֹ��ʼ�ͷţ��ڰ�AB�뿪�ų�ǰ�Ѿ�������ֱ���˶��������������ʼ�ձ���ˮƽ�����뵼��Ӵ����ã���֪�������ٶ�Ϊg�����AB��ͨ���ų�����Ĺ����У�����˵����ȷ���ǣ�������| A�� | ͨ��R�ĵ����Ϊq=$\frac{BLd}{R+r}$ | |
| B�� | �뿪�ų�˲�䣬��AB���ٶȴ�СΪv=$\frac{mg��R+r��}{{B}^{2}{L}^{2}}$ | |
| C�� | �ù����а����������Ĺ�ΪW=mg��h+d��-$\frac{{m}^{2}{g}^{2}��R+r��^{2}}{2{B}^{2}{L}^{2}}$ | |
| D�� | ��h��$\frac{{m}^{2}g��R+r��^{2}}{2{B}^{4}{L}^{4}}$ʱ��������ų����ȼ��ٺ����� |
 ��ͼ��������AOBΪ����ֱ�����⾵�ĺ���棬��OA��OBΪ�Ὠ��ֱ������ϵxoy��OA=OB=L���⾵��������Ϊn=$\sqrt{2}$��һ��ƽ����б��AB��ƽ�й��OB�����룮�����⾵ֻ����һ���ڲ����䣮
��ͼ��������AOBΪ����ֱ�����⾵�ĺ���棬��OA��OBΪ�Ὠ��ֱ������ϵxoy��OA=OB=L���⾵��������Ϊn=$\sqrt{2}$��һ��ƽ����б��AB��ƽ�й��OB�����룮�����⾵ֻ����һ���ڲ����䣮 ���ļ�����һ�ַdz��̼��Ļ��������˶����˴�ˮ���Ϸ�ij����ƽ̨�����£����������ܵ����������������䣬������ıļ����ֻ�������ϵ�������������ȥ��Ȼ���������䣮���������������µ��˶��У��ļ�����ᵽ���Ķ��ǵĴ̼�����һ�αļ������õ���Ƥ��ԭ��Ϊ15 m������Ϊ50kg���������䵽��͵�ʱ���ܵ����ϵ��������Ϊ3000N����֪����ͣ�ڿ���ʱ���ļ�����Ƥ������Ϊ17.5 m����Ƥ���ĵ������쳤�Ĺ�ϵ���Ϻ��˶��ɣ���ȡg=10 N/kg������
���ļ�����һ�ַdz��̼��Ļ��������˶����˴�ˮ���Ϸ�ij����ƽ̨�����£����������ܵ����������������䣬������ıļ����ֻ�������ϵ�������������ȥ��Ȼ���������䣮���������������µ��˶��У��ļ�����ᵽ���Ķ��ǵĴ̼�����һ�αļ������õ���Ƥ��ԭ��Ϊ15 m������Ϊ50kg���������䵽��͵�ʱ���ܵ����ϵ��������Ϊ3000N����֪����ͣ�ڿ���ʱ���ļ�����Ƥ������Ϊ17.5 m����Ƥ���ĵ������쳤�Ĺ�ϵ���Ϻ��˶��ɣ���ȡg=10 N/kg������ ��ͼ��ʾ����ǿ�ų���ֱ�ھ����߿�abcd���ų��ĴŸ�Ӧǿ��ΪB���������ΪS����ʹ���ο���ab��Ϊ��ת��90��ǣ�������������У������߿�Ĵ�ͨ���仯������ֵ��BS��
��ͼ��ʾ����ǿ�ų���ֱ�ھ����߿�abcd���ų��ĴŸ�Ӧǿ��ΪB���������ΪS����ʹ���ο���ab��Ϊ��ת��90��ǣ�������������У������߿�Ĵ�ͨ���仯������ֵ��BS�� n=100�ѵ�Բ����Ȧ��������ͼ��ʾ�Ĵų��ڣ���Ȧ�ұߵĵ�·��û�дų������ų�����������Ȧ��ͨ���ı仯��$\frac{����}{��t}$=0.004 Wb/s����Ȧ����r=1����R=3������
n=100�ѵ�Բ����Ȧ��������ͼ��ʾ�Ĵų��ڣ���Ȧ�ұߵĵ�·��û�дų������ų�����������Ȧ��ͨ���ı仯��$\frac{����}{��t}$=0.004 Wb/s����Ȧ����r=1����R=3������