题目内容
18.质量m=4kg的物体,与水平地面间的动摩擦因数μ=0.1,沿水平地面向右做直线运动,经过A点时速度为6m/s.物体过A点时开始计时,对物体施加水平恒力F作用,经过0.5s物体向右移动了2.5m到达B点;若t时刻撤去水平恒力F,物体最后停在A的右方6.0m处.重力加速度g=10m/s2.求:(1)撤去水平恒力F的时刻t;
(2)从物体经过A点到最终停止,水平恒力F做的功WF.
分析 (1)研究AB段,由位移公式求出加速度.再对A到物体停止的整个过程,运用速度位移公式列式,可求得恒力作用的时间.
(2)对整个过程,运用动能定理求恒力做功.
解答 解:(1)物体从A运动到B的过程,由xAB=vAt+$\frac{1}{2}a{t}^{2}$得:
代入数据得:2.5=6×0.5+$\frac{1}{2}$×a×0.52;
解得:a=-4m/s2.
撤去F后物体的加速度大小为:a′=$\frac{μmg}{m}$=1m/s2.
设刚撤去F时物体的速度为v.
对整个过程有:x=$\frac{{v}^{2}-{v}_{A}^{2}}{2a}$+$\frac{{v}^{2}}{2a′}$
代入得:6.0=$\frac{{v}^{2}-{6}^{2}}{2×(-4)}$+$\frac{{v}^{2}}{2×1}$
解得:v=2m/s
则有:t=$\frac{v-{v}_{A}}{a}$=$\frac{2-6}{-4}$=1s
(2)从物体经过A点到最终停止,由动能定理得:
WF-μmgx=0-$\frac{1}{2}m{v}_{A}^{2}$
解得:WF=-56J
答:(1)撤去水平恒力F的时刻t是1s;
(2)从物体经过A点到最终停止,水平恒力F做的功WF是-56J.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁.运用动能定理时要灵活选取研究的过程.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.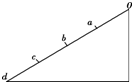 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d…,下列说法不正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| C. | 在斜面上运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |
13.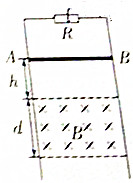 如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )
如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )
 如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )
如图所示,两根电阻不计、间距为L的光滑金属导轨竖直放置,导轨上端接电阻R,一质量为m,电阻为r的导体棒AB垂直放在导轨上,在距AB棒下方h处,在两导轨间矩形区域内分布有磁感应强度为B的匀强磁场,磁场方向垂直导轨平面向里,宽度为d,现使棒AB由静止开始释放,在棒AB离开磁场前已经做匀速直线运动,棒下落过程中始终保持水平,并与导轨接触良好,已知重力加速度为g,则棒AB在通过磁场区域的过程中,下列说法正确的是( )| A. | 通过R的电荷量为q=$\frac{BLd}{R+r}$ | |
| B. | 离开磁场瞬间,棒AB的速度大小为v=$\frac{mg(R+r)}{{B}^{2}{L}^{2}}$ | |
| C. | 该过程中安培力所做的功为W=mg(h+d)-$\frac{{m}^{2}{g}^{2}(R+r)^{2}}{2{B}^{2}{L}^{2}}$ | |
| D. | 当h<$\frac{{m}^{2}g(R+r)^{2}}{2{B}^{4}{L}^{4}}$时,棒进入磁场后先减速后匀速 |
3.最早发表有关碰撞问题研究成果的是( )
| A. | 牛顿 | B. | 伽利略 | C. | 惠更新 | D. | 马尔西 |
7. 如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
 如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )
如图所示,匀强电场中有a、b、c、d四点,四点刚好构成一个矩形,已知∠acd=30°,电场方向与矩形所在平面平行,已知a、d和c点的电势分别为(4-$\sqrt{3}$)V、4V和(4+$\sqrt{3}$)V,则( )| A. | 电场线与ac直线平行 | B. | 电场方向与ac直线垂直 | ||
| C. | b点电势为3V | D. | b、d位于同一等势面上 |
5. 如图所示,一物体自倾角为θ的固定斜面顶端水平抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足( )
如图所示,一物体自倾角为θ的固定斜面顶端水平抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足( )
 如图所示,一物体自倾角为θ的固定斜面顶端水平抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足( )
如图所示,一物体自倾角为θ的固定斜面顶端水平抛出后落在斜面上,物体与斜面接触时速度与水平方向的夹角φ满足( )| A. | tanφ=sinθ | B. | tanφ=2tanθ | C. | 2tanφ=tanθ | D. | tanφ=cosθ |
 如图所示,匀强磁场垂直于矩形线框abcd,磁场的磁感应强度为B,矩形面积为S.现使矩形框以ab边为轴转动90°角,则在这个过程中,穿过线框的磁通量变化量的数值是BS.
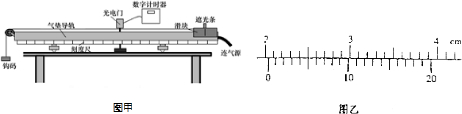
如图所示,匀强磁场垂直于矩形线框abcd,磁场的磁感应强度为B,矩形面积为S.现使矩形框以ab边为轴转动90°角,则在这个过程中,穿过线框的磁通量变化量的数值是BS. 物体做匀速圆周运动时,向心力与哪些因素有关?某同学通过下面实验探究,获得体验.
物体做匀速圆周运动时,向心力与哪些因素有关?某同学通过下面实验探究,获得体验.