题目内容
20．
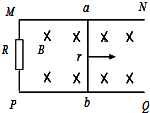图中磁场的磁感应强度B=1T，平行导轨宽L=1m，R=1Ω，金属棒ab以1m/s的速度紧贴导轨向右运动，其他电阻不计，试求通过R的电流大小和方向．
分析 根据法拉第电磁感应定律和闭合电路的欧姆定律求解感应电流，根据右手定则判断电流方向．
解答 解：根据导体切割磁感应线产生的感应电动势的计算公式可得：
E=BLv=1×1×1=1V，
根据欧姆定律可得电流为：
I=$\frac{E}{R}=\frac{1}{1}$A=1A，
根据右手定则可得电流方向为M→P．
答：金属棒ab中通过的电流为1A，方向为M→P．
点评 本题考查了求感应电流，分析清楚导体棒的运动情况，应用E=BLv、欧姆定律．右手定则可以解题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
如图所示，半圆形玻璃砖的半径为R，AB边水平且与x轴重合，在纸面内的一束单色光从玻璃砖的C点射入，入射角θ可从0°到90°变化，现只考虑能从AB边折射的情况（不考虑从AB上反射后的情况）．已知：α=45°，玻璃砖对该单色光的折射率n=$\sqrt{2}$，光在真空中的速度为c．求；
15．
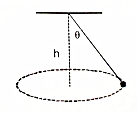如图所示，圆锥摆的摆球质量为m，摆球悬挂点到轨迹圆的圆心的距离为h，当摆球以某一线速度在水平面内做匀速圆周运动时，摆线与竖直方向的夹角为θ，若不计空气阻力的影响，重力加速度为g，则下面有关判断中正确的是（ ）
如图所示，圆锥摆的摆球质量为m，摆球悬挂点到轨迹圆的圆心的距离为h，当摆球以某一线速度在水平面内做匀速圆周运动时，摆线与竖直方向的夹角为θ，若不计空气阻力的影响，重力加速度为g，则下面有关判断中正确的是（ ）| A． | 摆线上的张力大小等于mgcosθ | B． | 摆球的向心力大小等于mgtanθ | ||
| C． | 摆球的线速度大小等于$\sqrt{ghtanθ}$ | D． | 摆球的周期等于2π$\sqrt{\frac{h}{g}}$ |
8．如图所示，用相同导线制成的边长为L或2L的四个单匝闭合回路，它们以相同的速度先后垂直穿过正方向匀强磁场区域，磁场方向垂直纸面向外，区域宽度大于2L，则在回路进入磁场的过程中，电流相等的回路是（ ）
| A． | 甲和乙 | B． | 乙和丙 | C． | 丙和丁 | D． | 甲和丁 |
15．
如图相距为L的两光滑平行导轨，平行放置在倾角为θ的斜面上，导轨的右端接有电阻R（轨道电阻不计），斜面处在一匀强磁场B中，磁场方向垂直于斜面向上，质量为m，电阻为R的金属棒ab放在导轨上，与导轨接触良好，由静止释放，下滑距离s后速度最大，则（ ）
如图相距为L的两光滑平行导轨，平行放置在倾角为θ的斜面上，导轨的右端接有电阻R（轨道电阻不计），斜面处在一匀强磁场B中，磁场方向垂直于斜面向上，质量为m，电阻为R的金属棒ab放在导轨上，与导轨接触良好，由静止释放，下滑距离s后速度最大，则（ ）| A． | 下滑过程电阻R消耗的最大功率为$\frac{{m}^{2}{g}^{2}si{n}^{2}θ}{{B}^{2}{L}^{2}}$R | |
| B． | 下滑过程电阻R消耗的最大功率为$\frac{3{m}^{2}{g}^{2}si{n}^{2}θ}{{B}^{2}{L}^{2}}$R | |
| C． | 下滑过程重力做功为mgssinθ | |
| D． | 下滑过程克服安培力做的功为$\frac{9{m}^{3}{g}^{2}si{n}^{2}θ}{2{B}^{4}{L}^{4}}$R2 |
如图所示，OACO为置于水平面内的光滑闭合金属导轨，OCA导轨的形状满足方程y=1.0sin（$\frac{π}{3}$x）（单位：m）．O、C处分别接有短电阻丝（图中粗线表法），R1=3.0Ω、R2=6.0Ω（导轨其它部分电阻不计）．在xOy内存在B=0.2T的匀强磁场，方向如图．现有一长1.5m的金属棒在水平外力F作用下以速度v=5.0m/s水平向右匀速运动．在设棒与导轨接触良好，不计棒的电阻．求：
12．
如图所示，用粗细相同的铜丝做成边长分别为L和3L的两只闭合线框a和b，现将两线框分别以va、vb的速度从磁感应强度为B的匀强磁场区域中匀速地拉到磁场外，若va=2vb，则在此过程中外力对线框做的功分别为Wa、Wb，通过两导体框某一截面的电量分别为Qa、Qb，则（ ）
如图所示，用粗细相同的铜丝做成边长分别为L和3L的两只闭合线框a和b，现将两线框分别以va、vb的速度从磁感应强度为B的匀强磁场区域中匀速地拉到磁场外，若va=2vb，则在此过程中外力对线框做的功分别为Wa、Wb，通过两导体框某一截面的电量分别为Qa、Qb，则（ ）| A． | Wa：Wb=2：27 | B． | Wa：Wb=2：9 | C． | Qa、Qb=1：9 | D． | Qa、Qb=1：3 |
如图所示，两根电阻不计、相距L且足够长的平行光滑导轨与水平面成 θ 角，导轨处在磁感应强度B的匀强磁场中，磁场方向垂直导轨平面斜向上，导轨下端连接阻值为R的电阻．现让一质量为m，电阻也为R、与导轨接触良好的水平金属棒ab从静止开始下滑，ab下滑距离s后开始匀速运动，重力加速度为g．求：
如图所示为电子技术中常用的电路之一．“～”表示低频交流，“～～～～”表示高频交流，“-”表示直流，则下列叙述正确的是（ ）