题目内容
5. 如图所示,OACO为置于水平面内的光滑闭合金属导轨,OCA导轨的形状满足方程y=1.0sin($\frac{π}{3}$x)(单位:m).O、C处分别接有短电阻丝(图中粗线表法),R1=3.0Ω、R2=6.0Ω(导轨其它部分电阻不计).在xOy内存在B=0.2T的匀强磁场,方向如图.现有一长1.5m的金属棒在水平外力F作用下以速度v=5.0m/s水平向右匀速运动.在设棒与导轨接触良好,不计棒的电阻.求:
如图所示,OACO为置于水平面内的光滑闭合金属导轨,OCA导轨的形状满足方程y=1.0sin($\frac{π}{3}$x)(单位:m).O、C处分别接有短电阻丝(图中粗线表法),R1=3.0Ω、R2=6.0Ω(导轨其它部分电阻不计).在xOy内存在B=0.2T的匀强磁场,方向如图.现有一长1.5m的金属棒在水平外力F作用下以速度v=5.0m/s水平向右匀速运动.在设棒与导轨接触良好,不计棒的电阻.求:(1)外力F的最大值;
(2)金属棒在导轨上运动时R1消耗的最大电功率;
(3)金属棒滑动导轨的过程中,外力所做的功.
分析 (1)金属棒在导轨上从O点滑动到A点,切割磁感线产生电动势,有效切割长度y按正弦规律变化,当y最大时,感应电流最大,安培力最大,外力F最大.棒做匀速运动,外力始终与安培力平衡,当感应电流最大时,安培力最大,则外力也最大,由F=BIL公式求出外力的最大值;
(2)当y最大时,感应电流最大,电阻丝R1上消耗的功率最大.根据电功率计算公式求解R1的最大功率;
(3)金属棒滑过导轨OA的过程,外力所做的功等于电路中产生的焦耳热,根据焦耳定律求解.
解答 解:(1)金属棒滑至C处,有效切割长度最大,金属棒上感应电动势最大,
由于y=1.0sin($\frac{π}{3}$x),令y=0,有OA长度为xA=3m
金属棒滑至C点时有:xC=$\frac{{x}_{A}}{2}$=1.5m
故yC=1.0sin($\frac{π}{3}$×1.5)m=1.0m
电路总电阻为:R总=$\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$=2Ω
感应电动势为:EC=ByCv
感应电流最大值为 Im=$\frac{{E}_{c}}{{R}_{总}}$=0.5A
金属棒匀速通过金属导轨C处时,外力有最大值为:
Fm=BImyC=0.2×0.5×1N=0.1N;
(2)通过电阻R1的电流为:I1=$\frac{{R}_{2}}{{R}_{1}+{R}_{2}}{I}_{m}$=$\frac{1}{3}$A
R1的最大功率为:P1m=I12R1=0.33W
(3)根据法拉第电磁感应定律可得:E=Byv=Bv•1.0sin($\frac{π}{3}$x),
而x=vt
所以得:E=1.0sin$\frac{5π}{3}$t(V),
所以感应电动势有效值为:
E有=$\frac{{E}_{m}}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$V,
t=$\frac{{x}_{A}}{v}$=0.6s
由能量守恒得:W外=Q=$\frac{{E}_{有}^{2}}{{R}_{总}}t$=0.15J
答:(1)外力F的最大值为0.1N;
(2)金属棒在导轨上运动时R1消耗的最大电功率为0.33W;
(3)金属棒滑动导轨的过程中,外力所做的功为0.15J.
点评 本题是产生正弦式电流的一种方式,运用电磁感应的基本规律得到感应电动势和感应电流的表达式,要注意的是求焦耳热时要用电流的有效值.

 阅读快车系列答案
阅读快车系列答案 在水平面上固定两个相互紧靠的三角形斜面,将a、b、c三个小球从左边斜面的顶点以不同的初速度向右水平抛出,落在斜面上时其落点如图所示,小球a落点距水平面的高度最低.下列判断正确的是( )
在水平面上固定两个相互紧靠的三角形斜面,将a、b、c三个小球从左边斜面的顶点以不同的初速度向右水平抛出,落在斜面上时其落点如图所示,小球a落点距水平面的高度最低.下列判断正确的是( )| A. | 小球c的初速度最小 | |
| B. | 小球a的飞行时间最长 | |
| C. | 小球c的整个飞行过程速度变化量最大 | |
| D. | 若减小小球a的初速度,其整个飞行过程速度变化量增大 |
 如图所示,MN、PQ是与水平面成θ角的两条平行光滑且足够长的金属轨道,其电阻忽略不计.空间存在着垂直于轨道平面向上的匀强磁场,磁感应强度大小为B.导体棒ab、cd垂直于轨道放置,且与轨道接触良好,每根导体棒的质量均为m,电阻均为R,轨道宽度为L,与轨道平行的绝缘细线一端固定,另一端与ab棒中点连接,细线承受的最大拉力Tm=2mgsinθ.今将cd棒由静止释放,则细线被拉断时( )
如图所示,MN、PQ是与水平面成θ角的两条平行光滑且足够长的金属轨道,其电阻忽略不计.空间存在着垂直于轨道平面向上的匀强磁场,磁感应强度大小为B.导体棒ab、cd垂直于轨道放置,且与轨道接触良好,每根导体棒的质量均为m,电阻均为R,轨道宽度为L,与轨道平行的绝缘细线一端固定,另一端与ab棒中点连接,细线承受的最大拉力Tm=2mgsinθ.今将cd棒由静止释放,则细线被拉断时( )| A. | cd棒的加速度大小是零 | B. | cd棒的速度大小是$\frac{2mgRsinθ}{{B}^{2}{L}^{2}}$ | ||
| C. | 流过ab棒的电流大小是$\frac{mgRsinθ}{BL}$ | D. | ab棒的发热功率为零 |
| A. | W1=W2,P1=P2 | B. | W2=2W1,P2=4P1 | C. | Q2=2Q1,q1= q2 | D. | Q2=Q1,2q1=q2 |

| A. | 据图可以算出恒力F的大小为10N | |
| B. | 据图可以估算出任意时间内电阻R上产生的热量 | |
| C. | 金属杆运动速度v=2.0m/s时的加速度a=4m/s2 | |
| D. | 金属杆运动速度v=2.0m/s时的加速度a=2.5m/s2 |
| A. | 卢瑟福发现了天然放射现象,揭示原子核有复杂的结构 | |
| B. | 比结合能越大,原子核中核子结合得越牢固,原子核越稳定 | |
| C. | 采用物理或化学方法可以有效地改变放射性元素的半衰期 | |
| D. | 原子核所含核子单独存在时的总质量小于该原子核的质量 |
 如图所示,在同一水平面上的两根光滑绝缘轨道,左侧间距为2l,右侧间距为l,有界匀强磁场仅存在于两轨道间,磁场的左右边界(图中虚线)均与轨道垂直.矩形金属线框abcd平放在轨道上,ab边长为l,bc边长为2l.开始时,bc边与磁场左边界的距离为2l,现给金属线框施加一个水平向右的恒定拉力,金属线框由静止开始沿着两根绝缘轨道向右运动,且bc边始终与轨道垂直,从bc边进入磁场直到ad边进入磁场前,线框做匀速运动,从bc边进入右侧窄磁场区域直到ad边完全离开磁场之前,线框又做匀速运动.线框从开始运动到完全离开磁场前的整个过程中产生的热量为Q.问:
如图所示,在同一水平面上的两根光滑绝缘轨道,左侧间距为2l,右侧间距为l,有界匀强磁场仅存在于两轨道间,磁场的左右边界(图中虚线)均与轨道垂直.矩形金属线框abcd平放在轨道上,ab边长为l,bc边长为2l.开始时,bc边与磁场左边界的距离为2l,现给金属线框施加一个水平向右的恒定拉力,金属线框由静止开始沿着两根绝缘轨道向右运动,且bc边始终与轨道垂直,从bc边进入磁场直到ad边进入磁场前,线框做匀速运动,从bc边进入右侧窄磁场区域直到ad边完全离开磁场之前,线框又做匀速运动.线框从开始运动到完全离开磁场前的整个过程中产生的热量为Q.问: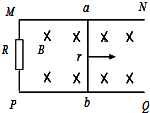 图中磁场的磁感应强度B=1T,平行导轨宽L=1m,R=1Ω,金属棒ab以1m/s的速度紧贴导轨向右运动,其他电阻不计,试求通过R的电流大小和方向.
图中磁场的磁感应强度B=1T,平行导轨宽L=1m,R=1Ω,金属棒ab以1m/s的速度紧贴导轨向右运动,其他电阻不计,试求通过R的电流大小和方向.