题目内容
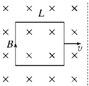
14. 如图所示,MN、PQ是两条彼此平行的金属导轨,水平放置,距离L为1米,匀强磁场的磁感线垂直导轨平面,B=2T.导轨左端连接一阻值R=1.5Ω的电阻,电阻两端并联一电压表,在导轨上垂直导轨跨接一金属杆ab,ab的质量m=1kg,电阻为r=0.5Ω,ab与导轨间动摩擦因数μ=0.5,导轨电阻不计.现用大小恒定的力F=9N水平向右拉ab运动,经一段时间后,ab开始匀速运动,此时其移动了2m:
如图所示,MN、PQ是两条彼此平行的金属导轨,水平放置,距离L为1米,匀强磁场的磁感线垂直导轨平面,B=2T.导轨左端连接一阻值R=1.5Ω的电阻,电阻两端并联一电压表,在导轨上垂直导轨跨接一金属杆ab,ab的质量m=1kg,电阻为r=0.5Ω,ab与导轨间动摩擦因数μ=0.5,导轨电阻不计.现用大小恒定的力F=9N水平向右拉ab运动,经一段时间后,ab开始匀速运动,此时其移动了2m:(1)求ab匀速运动时的速度
(2)求此时伏特表的读数
(3)求从ab开始运动到ab匀速运动的过程中,电路中的电热能.
分析 (1)抓住ab棒的合力为零,结合平衡,运用切割产生的感应电动势公式、闭合电路欧姆定律、安培力公式求出ab匀速运动的速度.
(2)根据切割产生的感应电动势公式、结合闭合电路欧姆定律求出伏特表的示数.
(3)根据能量守恒定律求出电路中的电热能.
解答 解:(1)当ab棒匀速运动时,有:F=μmg+FA,
又${F}_{A}=BIL=\frac{{B}^{2}{L}^{2}v}{R+r}$,
整理得,$F=μmg+\frac{{B}^{2}{L}^{2}v}{R+r}$,
解得ab匀速运动的速度v=$\frac{(F-μmg)(R+r)}{{B}^{2}{L}^{2}}$=$\frac{(9-0.5×10)×2}{4×1}m/s=2m/s$.
(2)伏特表的读数U=$\frac{BLv}{R+r}R=\frac{2×1×2}{2}×1.5V=3V$.
(3)根据能量守恒得,$Fs=Q+μmgs+\frac{1}{2}m{v}^{2}$,
代入数据解得Q=6J.
答:(1)ab匀速运动时的速度为2m/s;
(2)求此时伏特表的读数为3V;
(3)电路中的电热能为6J.
点评 本题考查了电磁感应与力学、电路和能量的综合运用,掌握切割产生的感应电动势公式、闭合电路欧姆定律和安培力公式是解决本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
5. 如图所示,边长为L的正方形闭合导线框置于磁感应强度为B的匀强磁场中,线框平面与磁感线的方向垂直.用力将线框分别以速度v1和v2匀速拉出磁场,比较这两个过程,以下判断正确的是( )
如图所示,边长为L的正方形闭合导线框置于磁感应强度为B的匀强磁场中,线框平面与磁感线的方向垂直.用力将线框分别以速度v1和v2匀速拉出磁场,比较这两个过程,以下判断正确的是( )
 如图所示,边长为L的正方形闭合导线框置于磁感应强度为B的匀强磁场中,线框平面与磁感线的方向垂直.用力将线框分别以速度v1和v2匀速拉出磁场,比较这两个过程,以下判断正确的是( )
如图所示,边长为L的正方形闭合导线框置于磁感应强度为B的匀强磁场中,线框平面与磁感线的方向垂直.用力将线框分别以速度v1和v2匀速拉出磁场,比较这两个过程,以下判断正确的是( )| A. | 若v1>v2,通过线框导线的电荷量q1>q2 | |
| B. | 若v1>v2,拉力F1<F2 | |
| C. | 若v1=2v2,拉力作用的功率P1=2P2 | |
| D. | 若v1=2v2,拉力所做的功W1=2W2 |
2. 如图所示,倾角为α的固定斜面下端固定一挡板,一劲度系数为k的轻弹簧下端固定在挡板上,现将一质量为m的小物块从斜面上离弹簧上端距离为s处,由静止释放,已知物块与斜面间的动摩擦因数为μ(μ<tanα),物块下滑过程中的最大动能为Ekm,则小物块从释放到运动至最低点的过程中,下列说法中正确的是( )
如图所示,倾角为α的固定斜面下端固定一挡板,一劲度系数为k的轻弹簧下端固定在挡板上,现将一质量为m的小物块从斜面上离弹簧上端距离为s处,由静止释放,已知物块与斜面间的动摩擦因数为μ(μ<tanα),物块下滑过程中的最大动能为Ekm,则小物块从释放到运动至最低点的过程中,下列说法中正确的是( )
 如图所示,倾角为α的固定斜面下端固定一挡板,一劲度系数为k的轻弹簧下端固定在挡板上,现将一质量为m的小物块从斜面上离弹簧上端距离为s处,由静止释放,已知物块与斜面间的动摩擦因数为μ(μ<tanα),物块下滑过程中的最大动能为Ekm,则小物块从释放到运动至最低点的过程中,下列说法中正确的是( )
如图所示,倾角为α的固定斜面下端固定一挡板,一劲度系数为k的轻弹簧下端固定在挡板上,现将一质量为m的小物块从斜面上离弹簧上端距离为s处,由静止释放,已知物块与斜面间的动摩擦因数为μ(μ<tanα),物块下滑过程中的最大动能为Ekm,则小物块从释放到运动至最低点的过程中,下列说法中正确的是( )| A. | 物块的最大动能Ekm等于对应过程中重力与摩擦力对物块做功之和 | |
| B. | 弹簧的最大弹性势能等于整个过程中重力与摩擦力对物块做功之和 | |
| C. | 当物块的最大动能为Ekm时,弹簧的压缩量x=$\frac{mgsinα-μmgcosα}{k}$ | |
| D. | 若将物块从离弹簧上端2s的斜面上由静止释放,则下滑过程中物块的最大动能等于2Ekm |
9. 一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )
一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )
 一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )
一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )| A. | 若水平力F是恒定的力,则力F所做的功为FLsinθ | |
| B. | 若水平力F是恒定的力,则力F所做的功为FL(1-cosθ) | |
| C. | 若是把小球缓慢移动,则力F所做的功为mgL(1-cosθ) | |
| D. | 若是把小球缓慢移动,则力F所做的功为FLsinθ |
19. 如图所示,在水平桌面上放置两条相距l的平行粗糙且无限长的金属导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.金属滑杆MN垂直于导轨并可在导轨上滑动,且与导轨始终接触良好.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.滑杆与导轨电阻不计,滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一质量为m的物块相连,拉滑杆的绳处于水平拉直状态.现若从静止开始释放物块,用I表示稳定后回路中的感应电流,g表示重力加速度,设滑杆在运动中所受的摩擦阻力恒为Ff,则在物块下落过程中( )
如图所示,在水平桌面上放置两条相距l的平行粗糙且无限长的金属导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.金属滑杆MN垂直于导轨并可在导轨上滑动,且与导轨始终接触良好.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.滑杆与导轨电阻不计,滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一质量为m的物块相连,拉滑杆的绳处于水平拉直状态.现若从静止开始释放物块,用I表示稳定后回路中的感应电流,g表示重力加速度,设滑杆在运动中所受的摩擦阻力恒为Ff,则在物块下落过程中( )
 如图所示,在水平桌面上放置两条相距l的平行粗糙且无限长的金属导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.金属滑杆MN垂直于导轨并可在导轨上滑动,且与导轨始终接触良好.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.滑杆与导轨电阻不计,滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一质量为m的物块相连,拉滑杆的绳处于水平拉直状态.现若从静止开始释放物块,用I表示稳定后回路中的感应电流,g表示重力加速度,设滑杆在运动中所受的摩擦阻力恒为Ff,则在物块下落过程中( )
如图所示,在水平桌面上放置两条相距l的平行粗糙且无限长的金属导轨ab与cd,阻值为R的电阻与导轨的a、c端相连.金属滑杆MN垂直于导轨并可在导轨上滑动,且与导轨始终接触良好.整个装置放于匀强磁场中,磁场的方向竖直向上,磁感应强度的大小为B.滑杆与导轨电阻不计,滑杆的中点系一不可伸长的轻绳,绳绕过固定在桌边的光滑轻滑轮后,与一质量为m的物块相连,拉滑杆的绳处于水平拉直状态.现若从静止开始释放物块,用I表示稳定后回路中的感应电流,g表示重力加速度,设滑杆在运动中所受的摩擦阻力恒为Ff,则在物块下落过程中( )| A. | 物体的最终速度为$\frac{(mg-{F}_{f})R}{{B}^{2}{l}^{2}}$ | |
| B. | 物体的最终速度为$\frac{{I}^{2}R}{mg-{F}_{f}}$ | |
| C. | 物体重力的最大功率为$\frac{mg(mg{-F}_{f})R}{{B}^{2}{l}^{2}}$ | |
| D. | 物体重力的最大功率可能大于$\frac{{mg(mg-F}_{f})R}{{B}^{2}{l}^{2}}$ |
6.如图1所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为l,电阻均可忽略不计.在M和P之间接有阻值为R的定值电阻,导体杆ab质量为m、有效电阻为r,并与导轨接触良好.整个装置处于方向竖直向上磁感应强度为B的匀强磁场中.现给ab杆一个初速度v0,使杆向右运动.则( )

| A. | 当ab杆刚好具有初速度v0时,此时ab杆两端的电压 U=$\frac{{Blv}_{0}R}{R+r}$,且a端电势高于b端电势 | |
| B. | 通过电阻R的电流i随时间t 的变化率的绝对值逐渐增大 | |
| C. | 若将M和P之间的电阻R改为接一电容为C的电容器,如图2所示.同样给ab杆一个初速度v0,使杆向右运动,则ab杆稳定后的速度为v=$\frac{{mv}_{0}}{{m+{B}^{2}l}^{2}C}$ | |
| D. | 在C选项中,杆稳定后a端电势高于b端电势 |
4. 如图是打开的汽车后备箱掀盖,右图为简易侧视示意图,A为后盖顶端边缘上一点,B为后盖中间一点,整个后盖可绕固定于车身的铰链O转动.在合上后盖的过程中A、B两点做圆周运动,则图中时刻( )
如图是打开的汽车后备箱掀盖,右图为简易侧视示意图,A为后盖顶端边缘上一点,B为后盖中间一点,整个后盖可绕固定于车身的铰链O转动.在合上后盖的过程中A、B两点做圆周运动,则图中时刻( )
 如图是打开的汽车后备箱掀盖,右图为简易侧视示意图,A为后盖顶端边缘上一点,B为后盖中间一点,整个后盖可绕固定于车身的铰链O转动.在合上后盖的过程中A、B两点做圆周运动,则图中时刻( )
如图是打开的汽车后备箱掀盖,右图为简易侧视示意图,A为后盖顶端边缘上一点,B为后盖中间一点,整个后盖可绕固定于车身的铰链O转动.在合上后盖的过程中A、B两点做圆周运动,则图中时刻( )| A. | A点的线速度方向沿AO方向 | B. | A、B两点的线速度vA<vB | ||
| C. | A、B两点的角速度ωA<ωB | D. | A、B两点的向心加速度aA>aB |
