题目内容
9. 一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )
一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )| A. | 若水平力F是恒定的力,则力F所做的功为FLsinθ | |
| B. | 若水平力F是恒定的力,则力F所做的功为FL(1-cosθ) | |
| C. | 若是把小球缓慢移动,则力F所做的功为mgL(1-cosθ) | |
| D. | 若是把小球缓慢移动,则力F所做的功为FLsinθ |
分析 如果用恒力拉动物体,则根据功的公式直接求解拉力的功;
如果小球在水平拉力F的作用下,从平衡位置P点很缓慢地移动到Q点,动能不变,根据动能定理求出水平力F所做的功.
解答 解:AB、由于拉力为恒力,并且力始终沿水平方向,水平位移为lsinθ,所以WF=Flsinθ;故A正确,B错误;
CD、球在缓慢移动的过程中,水平力F是变力,不能通过功的公式求解功的大小,
根据动能定理得:WF-mgl(1-cosθ)=0,
解得水平力F所做的功为:WF=mgl(1-cosθ).故C正确,D错误.
故选:AC.
点评 本题关键是要注意恒力做功表达式的适用范围,题中是恒力,故直接用公式求解;如果改为缓慢移动,则力不是恒力,只能用动能定理列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )
一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )
 一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )
一个静止的放射性同位素的原子核${\;}_{15}^{30}$P衰变为${\;}_{14}^{30}$Si,另一个静止的天然放射性元素的原子核${\;}_{90}^{234}$Th衰变为${\;}_{91}^{234}$Pa,在同一磁场中,得到衰变后粒子的运动径迹1、2、3、4,如图所示,则这四条径迹依次是( )| A. | 图中1、2为${\;}_{90}^{234}$Th衰变产生的${\;}_{91}^{234}$Pa和${\;}_{-1}^{0}$e的轨迹,其中1是电子${\;}_{-1}^{0}$e的轨迹 | |
| B. | 图中1、2为${\;}_{15}^{30}$P衰变产生的${\;}_{14}^{30}$Si和${\;}_{1}^{0}$e的轨迹,其中2是正电子${\;}_{1}^{0}$e的轨迹 | |
| C. | 图中3、4是${\;}_{15}^{30}$P衰变产生的${\;}_{14}^{30}$Si和${\;}_{1}^{0}$e的轨迹,其中3是正电子${\;}_{1}^{0}$e的轨迹 | |
| D. | 图中3、4轨迹中两粒子在磁场中旋转方向相反 |
4. 如图所示,M1N1与M2N2是位于同一水平面内的两条平行金属导轨,导轨间距为L磁感应强度为B的匀强磁场与导轨所在平面垂直,ab与ef为两根金属杆,与导轨垂直且可在导轨上滑 动,金属杆ab上有一伏特表,除伏特表外,其他部分电阻可以不计,则下列说法正确的是( )
如图所示,M1N1与M2N2是位于同一水平面内的两条平行金属导轨,导轨间距为L磁感应强度为B的匀强磁场与导轨所在平面垂直,ab与ef为两根金属杆,与导轨垂直且可在导轨上滑 动,金属杆ab上有一伏特表,除伏特表外,其他部分电阻可以不计,则下列说法正确的是( )
 如图所示,M1N1与M2N2是位于同一水平面内的两条平行金属导轨,导轨间距为L磁感应强度为B的匀强磁场与导轨所在平面垂直,ab与ef为两根金属杆,与导轨垂直且可在导轨上滑 动,金属杆ab上有一伏特表,除伏特表外,其他部分电阻可以不计,则下列说法正确的是( )
如图所示,M1N1与M2N2是位于同一水平面内的两条平行金属导轨,导轨间距为L磁感应强度为B的匀强磁场与导轨所在平面垂直,ab与ef为两根金属杆,与导轨垂直且可在导轨上滑 动,金属杆ab上有一伏特表,除伏特表外,其他部分电阻可以不计,则下列说法正确的是( )| A. | 若ab固定ef以速度v滑动时,伏特表读数为BLv | |
| B. | 若ab固定ef以速度v滑动时,ef两点间电压为零 | |
| C. | 当两杆以相同的速度v同向滑动时,伏特表读数为BLv | |
| D. | 当两杆以相同的速度v同向滑动时,伏特表读数为2BLv |
18.如图甲所示,垂直纸面向里的有界匀强磁场磁感应强度B=1.0T,质量为m=0.04kg、高h=0.05m、总电阻R=5Ω、n=100匝的矩形线圈竖直固定在质量为M=0.08kg的小车上,小车与线圈的水平长度l相同.当线圈和小车一起沿光滑水平面运动,并以初速度v1=10m/s进入磁场,线圈平面和磁场方向始终垂直.若小车运动的速度v随车的位移x变化的v-x图象如图乙所示,则根据以上信息可知( )

| A. | 小车的水平长度l=15 cm | |
| B. | 磁场的宽度d=25cm | |
| C. | 小车的位移x=10 cm时线圈中的电流I=7 A | |
| D. | 线圈通过磁场的过程中线圈产生的热量Q=1.92J |
19. 在某地应用打点计时器做不同的实验时得到了四条纸带,已知每条纸带上相邻两个点的时间间隔均为0.02s,连续的相邻两个点的距离均用x1、x2、x3表示,如图所示.已知当地的重力加速度为9.8m/s2,下列数据中,符合利用自由落体运动验证机械能守恒定律实验的是( )
在某地应用打点计时器做不同的实验时得到了四条纸带,已知每条纸带上相邻两个点的时间间隔均为0.02s,连续的相邻两个点的距离均用x1、x2、x3表示,如图所示.已知当地的重力加速度为9.8m/s2,下列数据中,符合利用自由落体运动验证机械能守恒定律实验的是( )
 在某地应用打点计时器做不同的实验时得到了四条纸带,已知每条纸带上相邻两个点的时间间隔均为0.02s,连续的相邻两个点的距离均用x1、x2、x3表示,如图所示.已知当地的重力加速度为9.8m/s2,下列数据中,符合利用自由落体运动验证机械能守恒定律实验的是( )
在某地应用打点计时器做不同的实验时得到了四条纸带,已知每条纸带上相邻两个点的时间间隔均为0.02s,连续的相邻两个点的距离均用x1、x2、x3表示,如图所示.已知当地的重力加速度为9.8m/s2,下列数据中,符合利用自由落体运动验证机械能守恒定律实验的是( )| A. | x1=41.2mm,x2=43.1mm,x3=45.0mm | B. | x1=49.3mm,x2=53.2mm,x3=57.1mm | ||
| C. | x1=61.0mm,x2=65.8mm,x3=70.7mm | D. | x1=60.5mm,x2=61.0mm,x3=60.6mm |

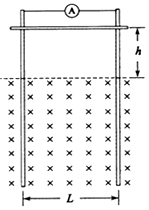 如图所示,两根足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.磁感应强度为B,一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求:
如图所示,两根足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.磁感应强度为B,一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求: 如图所示,MN、PQ是两条彼此平行的金属导轨,水平放置,距离L为1米,匀强磁场的磁感线垂直导轨平面,B=2T.导轨左端连接一阻值R=1.5Ω的电阻,电阻两端并联一电压表,在导轨上垂直导轨跨接一金属杆ab,ab的质量m=1kg,电阻为r=0.5Ω,ab与导轨间动摩擦因数μ=0.5,导轨电阻不计.现用大小恒定的力F=9N水平向右拉ab运动,经一段时间后,ab开始匀速运动,此时其移动了2m:
如图所示,MN、PQ是两条彼此平行的金属导轨,水平放置,距离L为1米,匀强磁场的磁感线垂直导轨平面,B=2T.导轨左端连接一阻值R=1.5Ω的电阻,电阻两端并联一电压表,在导轨上垂直导轨跨接一金属杆ab,ab的质量m=1kg,电阻为r=0.5Ω,ab与导轨间动摩擦因数μ=0.5,导轨电阻不计.现用大小恒定的力F=9N水平向右拉ab运动,经一段时间后,ab开始匀速运动,此时其移动了2m: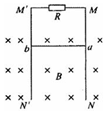 示,两根光滑的足够长直金属导轨MN、M′N′平行置于竖直面内,导轨间距为L,导轨上端接有阻值为R的电阻.质量为m、长度也为L、阻值为r的金属棒ab垂直于导轨放置,且与导轨保持良好接触,其他电阻不计.导轨处于磁感应强度为B、方向水平向里的匀强磁场中,现将ab棒由静止释放,在重力作用下向下运动,求:金属棒ab在运动过程中的最大速度.
示,两根光滑的足够长直金属导轨MN、M′N′平行置于竖直面内,导轨间距为L,导轨上端接有阻值为R的电阻.质量为m、长度也为L、阻值为r的金属棒ab垂直于导轨放置,且与导轨保持良好接触,其他电阻不计.导轨处于磁感应强度为B、方向水平向里的匀强磁场中,现将ab棒由静止释放,在重力作用下向下运动,求:金属棒ab在运动过程中的最大速度.