题目内容
6.如图1所示,水平面上有两根足够长的光滑平行金属导轨MN和PQ,两导轨间距为l,电阻均可忽略不计.在M和P之间接有阻值为R的定值电阻,导体杆ab质量为m、有效电阻为r,并与导轨接触良好.整个装置处于方向竖直向上磁感应强度为B的匀强磁场中.现给ab杆一个初速度v0,使杆向右运动.则( )
| A. | 当ab杆刚好具有初速度v0时,此时ab杆两端的电压 U=$\frac{{Blv}_{0}R}{R+r}$,且a端电势高于b端电势 | |
| B. | 通过电阻R的电流i随时间t 的变化率的绝对值逐渐增大 | |
| C. | 若将M和P之间的电阻R改为接一电容为C的电容器,如图2所示.同样给ab杆一个初速度v0,使杆向右运动,则ab杆稳定后的速度为v=$\frac{{mv}_{0}}{{m+{B}^{2}l}^{2}C}$ | |
| D. | 在C选项中,杆稳定后a端电势高于b端电势 |
分析 根据切割产生的感应电动势公式、闭合电路欧姆定律求出ab杆两端的电压,根据右手定则判断电势的高低.结合速度随时间的变化规律,根据切割产生的感应电动势公式得出电流的表达式,从而分析电流随时间的变化率的绝对值变化.
将M和P之间的电阻R改为接一电容为C的电容器,当ab杆稳定时,杆产生的电动势等于电容器两端的电压,结合电容器的定义式,运用动量定理,采用微元的思想求出ab杆稳定后的速度.
解答 解:A、当ab杆刚好具有初速度v0时,感应电动势E=Blv0,根据闭合电路欧姆定律得,ab杆两端的电压U=$\frac{E}{R+r}R=\frac{Bl{v}_{0}R}{R+r}$,根据右手定则知,感应电流的方向为b到a,a相当于电源的正极,则a点电势高于b点,故A正确.
B、通过电阻R的电流I=$\frac{BLv}{R+r}$,由于速度减小,则电流减小,安培力减小,做加速度减小的减速运动,速度随时间的切线斜率减小,则通过电阻R的电流i随时间t 的变化率的绝对值逐渐减小,故B错误.
C、当ab杆以初速度v0开始切割磁感线时,产生感应电动势,电路开始给电容器充电,有电流通过ab杆,杆在安培力的作用下做减速运动,随着速度减小,安培力减小,加速度也减小,杆做加速度减小的减速运动.当电容器两端电压与感应电动势相等时,充电结束,杆以恒定的速度做匀速直线运动,
电容器两端的电压U=Blv,
根据电容器电容C=$\frac{Q}{U}$,
ab杆为研究对象,在很短的一段时间△t内,杆受到的冲量大小为BIl△t
从ab杆开始运动至速度达到稳定的过程,根据动量定理:∑-BIl△t=-BlQ=mv-mv0
联立可得v=$\frac{m{v}_{0}}{m+{B}^{2}{l}^{2}C}$,故C正确.
D、稳定后,不再充电,回路中没有电流,根据右手定则知,a点的电动势高于b点,故D正确.
故选:ACD.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下物体的平衡问题;另一条是能量,分析电磁感应现象中的能量如何转化是关键.

| A. | 测量电阻时,表的指针偏转角度越大,误差就越小 | |
| B. | 更换测量挡时,需要重新调零 | |
| C. | 使用完毕应将选择开关旋至交流电压最高挡或“OFF”挡 | |
| D. | 欧姆表如果用×100Ω挡指针相对电流零刻度偏转太小,应改用×1kΩ挡或更高挡测量 |

| A. | 小车的水平长度l=15 cm | |
| B. | 磁场的宽度d=25cm | |
| C. | 小车的位移x=10 cm时线圈中的电流I=7 A | |
| D. | 线圈通过磁场的过程中线圈产生的热量Q=1.92J |
 如图所示,单匝线圈ABCD在外力F作用下以速度v向右匀速进入匀强磁场,第二次又以速度1.5v匀速进入同一个匀强磁场,则从CD边进入磁场开始到AB边进入磁场瞬间的整个过程中( )
如图所示,单匝线圈ABCD在外力F作用下以速度v向右匀速进入匀强磁场,第二次又以速度1.5v匀速进入同一个匀强磁场,则从CD边进入磁场开始到AB边进入磁场瞬间的整个过程中( )| A. | 第一次进入与第二次进入时线圈中外力F大小之比为1:1.5 | |
| B. | 第一次进入与第二次进入时线圈中安倍力做功大小之比为1:1.5 | |
| C. | 第一次进入与第二次进入时外力F做功的功率之比为1:(1.5)2 | |
| D. | 第一次进入与第二次进入时线圈中产生热量之比为1:(1.5)2 |
 在同一实验室中,甲、乙两水平弹簧振子的振动图象如图所示,则可知( )
在同一实验室中,甲、乙两水平弹簧振子的振动图象如图所示,则可知( )| A. | 振子甲速度为零时,振子乙速度最大 | |
| B. | 两振子的振动频率之比f甲:f乙=2:1 | |
| C. | 若将振子乙的振幅也增为10cm,则甲乙振子的振动周期会相等 | |
| D. | 任意2s内,甲乙两振子的路程相等 |
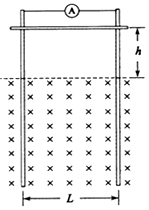 如图所示,两根足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.磁感应强度为B,一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求:
如图所示,两根足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.磁感应强度为B,一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求: 如图所示,MN、PQ是两条彼此平行的金属导轨,水平放置,距离L为1米,匀强磁场的磁感线垂直导轨平面,B=2T.导轨左端连接一阻值R=1.5Ω的电阻,电阻两端并联一电压表,在导轨上垂直导轨跨接一金属杆ab,ab的质量m=1kg,电阻为r=0.5Ω,ab与导轨间动摩擦因数μ=0.5,导轨电阻不计.现用大小恒定的力F=9N水平向右拉ab运动,经一段时间后,ab开始匀速运动,此时其移动了2m:
如图所示,MN、PQ是两条彼此平行的金属导轨,水平放置,距离L为1米,匀强磁场的磁感线垂直导轨平面,B=2T.导轨左端连接一阻值R=1.5Ω的电阻,电阻两端并联一电压表,在导轨上垂直导轨跨接一金属杆ab,ab的质量m=1kg,电阻为r=0.5Ω,ab与导轨间动摩擦因数μ=0.5,导轨电阻不计.现用大小恒定的力F=9N水平向右拉ab运动,经一段时间后,ab开始匀速运动,此时其移动了2m: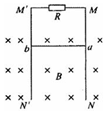 示,两根光滑的足够长直金属导轨MN、M′N′平行置于竖直面内,导轨间距为L,导轨上端接有阻值为R的电阻.质量为m、长度也为L、阻值为r的金属棒ab垂直于导轨放置,且与导轨保持良好接触,其他电阻不计.导轨处于磁感应强度为B、方向水平向里的匀强磁场中,现将ab棒由静止释放,在重力作用下向下运动,求:金属棒ab在运动过程中的最大速度.
示,两根光滑的足够长直金属导轨MN、M′N′平行置于竖直面内,导轨间距为L,导轨上端接有阻值为R的电阻.质量为m、长度也为L、阻值为r的金属棒ab垂直于导轨放置,且与导轨保持良好接触,其他电阻不计.导轨处于磁感应强度为B、方向水平向里的匀强磁场中,现将ab棒由静止释放,在重力作用下向下运动,求:金属棒ab在运动过程中的最大速度.



