题目内容
17.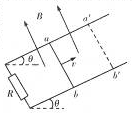 如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )
如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )| A. | 导体棒运动过程中的最大速度$\frac{mgsinθ}{{B}^{2}{l}^{2}}$ | |
| B. | R上的最大热功率为$\frac{{{m^2}{g^2}R{{sin}^2}θ}}{{{B^2}{l^2}}}$ | |
| C. | 导体棒返回到ab位置前已经达到下滑的最大速度 | |
| D. | 导体棒返回到ab位置时刚好达到下滑的最大速度 |
分析 当导体棒合力为零,速度最大,电流最大,热功率最大.上滑时的初始时刻,加速度最大,根据牛顿第二定律,结合切割产生的感应电动势公式、欧姆定律、安培力公式求出此时的速度,对全过程研究,运用能量守恒定律判断在何位置下滑的速度最大.
解答 解:A、当导体棒所受的合力为零时,速度最大,有:mgsinθ=$\frac{{B}^{2}{L}^{2}{v}_{m}}{R}$.解得vm=$\frac{mgRsinθ}{{B}^{2}{l}^{2}}$.故A错误.
B、当速度最大时,感应电流最大,R上的功率最大,则P=$\frac{{E}^{2}}{R}$=$\frac{(Bl{v}_{m})^{2}}{R}$=$\frac{{{m^2}{g^2}R{{sin}^2}θ}}{{{B^2}{l^2}}}$.故B正确.
CD、导体棒向上运动速度最大时,加速度最大,即在ab时的速度最大,设为v,根据牛顿第二定律得,mgsinθ+$\frac{{B}^{2}{l}^{2}v}{R}$=ma=2mgsinθ,则在ab时的速度v=$\frac{mgRsinθ}{{B}^{2}{l}^{2}}$,与下滑的最大速度相等,对从ab开始向上运动开始到下滑最大速度的过程中,由能量守恒定律得,动能变化量为零,则重力势能的减小量等于内能的产生.知导体棒返回到ab位置以下达到下滑的最大速度.故C、D错误.
故选:B.
点评 在分析下滑速度最大时的位置,抓住动能变化量为零,重力势能减小量等于内能的增加量分析.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
5. 某粒子分析器的简化结构如图.一束带电粒子(不计重力和粒子间的相互影响)从A小孔以特定的角度和初速度射入平行板电极P和Q之间的真空区域,经偏转后打在Q极板上如图所示的位置.在其他条件不变的情况下要使该粒子束能从Q极板上B孔射出,下列操作中可能实现的是( )
某粒子分析器的简化结构如图.一束带电粒子(不计重力和粒子间的相互影响)从A小孔以特定的角度和初速度射入平行板电极P和Q之间的真空区域,经偏转后打在Q极板上如图所示的位置.在其他条件不变的情况下要使该粒子束能从Q极板上B孔射出,下列操作中可能实现的是( )
 某粒子分析器的简化结构如图.一束带电粒子(不计重力和粒子间的相互影响)从A小孔以特定的角度和初速度射入平行板电极P和Q之间的真空区域,经偏转后打在Q极板上如图所示的位置.在其他条件不变的情况下要使该粒子束能从Q极板上B孔射出,下列操作中可能实现的是( )
某粒子分析器的简化结构如图.一束带电粒子(不计重力和粒子间的相互影响)从A小孔以特定的角度和初速度射入平行板电极P和Q之间的真空区域,经偏转后打在Q极板上如图所示的位置.在其他条件不变的情况下要使该粒子束能从Q极板上B孔射出,下列操作中可能实现的是( )| A. | 先断开开关S,再适当上移P极板 | B. | 先断开开关S,再适当左移P极板 | ||
| C. | 保持开关S闭合,适当上移P极板 | D. | 保持开关S闭合,适当左移P极板 |
12. 如图所示,质量为m的滑块在水平面上撞向弹簧,当滑块将弹簧压缩了x0时速度减小到零,然后弹簧又将滑块向右推开.已知弹簧的劲度系数为k,滑块与水平面间的动摩擦因数为μ,整个过程弹簧未超过弹性限度.则在滑块向左运动过程中,下列判断正确的是( )
如图所示,质量为m的滑块在水平面上撞向弹簧,当滑块将弹簧压缩了x0时速度减小到零,然后弹簧又将滑块向右推开.已知弹簧的劲度系数为k,滑块与水平面间的动摩擦因数为μ,整个过程弹簧未超过弹性限度.则在滑块向左运动过程中,下列判断正确的是( )
 如图所示,质量为m的滑块在水平面上撞向弹簧,当滑块将弹簧压缩了x0时速度减小到零,然后弹簧又将滑块向右推开.已知弹簧的劲度系数为k,滑块与水平面间的动摩擦因数为μ,整个过程弹簧未超过弹性限度.则在滑块向左运动过程中,下列判断正确的是( )
如图所示,质量为m的滑块在水平面上撞向弹簧,当滑块将弹簧压缩了x0时速度减小到零,然后弹簧又将滑块向右推开.已知弹簧的劲度系数为k,滑块与水平面间的动摩擦因数为μ,整个过程弹簧未超过弹性限度.则在滑块向左运动过程中,下列判断正确的是( )| A. | 滑块始终做加速运动 | |
| B. | 滑块始终做减速运动 | |
| C. | 当弹簧形变量x=$\frac{μmg}{k}$时,物体的加速度大小为2μg | |
| D. | 滑块与弹簧接触过程中最大加速度为$\frac{k{x}_{0}+μmg}{m}$ |
9. 上饶市云碧峰森林公园装有供游人休闲的吊床,吊床用绳子拴在两棵树上等高的位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳的拉力为F1、吊床对该人的作用力为F2,则( )
上饶市云碧峰森林公园装有供游人休闲的吊床,吊床用绳子拴在两棵树上等高的位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳的拉力为F1、吊床对该人的作用力为F2,则( )
 上饶市云碧峰森林公园装有供游人休闲的吊床,吊床用绳子拴在两棵树上等高的位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳的拉力为F1、吊床对该人的作用力为F2,则( )
上饶市云碧峰森林公园装有供游人休闲的吊床,吊床用绳子拴在两棵树上等高的位置.某人先坐在吊床上,后躺在吊床上,均处于静止状态.设吊床两端系绳的拉力为F1、吊床对该人的作用力为F2,则( )| A. | 坐着比躺着时F1大 | B. | 躺着比坐着时F1大 | ||
| C. | 坐着比躺着时F2大 | D. | 躺着与坐着时F2一样大 |
6. 如图所示,通过定滑轮悬挂两个质量为m1和m2的物体,其中m1>m2,不计绳子质量、绳子与滑轮间的摩擦等,当m1向下运动一段时间距离的过程中,下列说法正确的是( )
如图所示,通过定滑轮悬挂两个质量为m1和m2的物体,其中m1>m2,不计绳子质量、绳子与滑轮间的摩擦等,当m1向下运动一段时间距离的过程中,下列说法正确的是( )
 如图所示,通过定滑轮悬挂两个质量为m1和m2的物体,其中m1>m2,不计绳子质量、绳子与滑轮间的摩擦等,当m1向下运动一段时间距离的过程中,下列说法正确的是( )
如图所示,通过定滑轮悬挂两个质量为m1和m2的物体,其中m1>m2,不计绳子质量、绳子与滑轮间的摩擦等,当m1向下运动一段时间距离的过程中,下列说法正确的是( )| A. | m1势能的减少量等于m1动能的增加量 | |
| B. | m1势能的减少量等于m2势能的增加量 | |
| C. | m1势能的减少量等于m1与m2两者动能的增加量 | |
| D. | m1机械能的减少量等于m2机械能的增加量 |
7. 如图所示,a、b、c为静电场中一条直线上的三点,b为ac中点.a、c两点的电势分别为φa=6V、φc=2V.下列说法中正确的是( )
如图所示,a、b、c为静电场中一条直线上的三点,b为ac中点.a、c两点的电势分别为φa=6V、φc=2V.下列说法中正确的是( )
 如图所示,a、b、c为静电场中一条直线上的三点,b为ac中点.a、c两点的电势分别为φa=6V、φc=2V.下列说法中正确的是( )
如图所示,a、b、c为静电场中一条直线上的三点,b为ac中点.a、c两点的电势分别为φa=6V、φc=2V.下列说法中正确的是( )| A. | ab和bc之间的电势差大小关系一定为Uab=Ubc | |
| B. | 电场强度的方向一定为由a指向b | |
| C. | 正电荷在a点的电势能一定大于在c点的电势能 | |
| D. | a点的电场强度一定大于c点的电场强度 |
 如图所示,在平面直角坐标系xoy中,一半径为R圆形区域内有磁感应强度为B的匀强磁场,方向垂直纸面向外,圆形区域的圆心P在x轴上,OP=R.一质量为m、电量为q带正电的粒子从N点沿平行于x轴正方向进入匀强磁场,入射点N到x轴的距离为h,粒子重力不计.则:
如图所示,在平面直角坐标系xoy中,一半径为R圆形区域内有磁感应强度为B的匀强磁场,方向垂直纸面向外,圆形区域的圆心P在x轴上,OP=R.一质量为m、电量为q带正电的粒子从N点沿平行于x轴正方向进入匀强磁场,入射点N到x轴的距离为h,粒子重力不计.则: 如图所示,一个质量为m=2×10-15kg,电荷量为q=+3×10-10c的带电粒子(重力忽略不计),从静止开始经U1=90V电压加速后,由中点水平进入两水平平行金属板间的偏转电场,偏转电场的电压U2=70V,金属板长L=30$\sqrt{3}$cm,板间距离d=35cm.求
如图所示,一个质量为m=2×10-15kg,电荷量为q=+3×10-10c的带电粒子(重力忽略不计),从静止开始经U1=90V电压加速后,由中点水平进入两水平平行金属板间的偏转电场,偏转电场的电压U2=70V,金属板长L=30$\sqrt{3}$cm,板间距离d=35cm.求 质量为M的带支架的小车静止在光滑水平地面上,支架上用长为L的轻绳悬挂一质量为m的小球,现将小球拉至悬线水平位置后由静止释放,如图所示,试求在小球摆动过程中,小车的最大速度和最大位移.
质量为M的带支架的小车静止在光滑水平地面上,支架上用长为L的轻绳悬挂一质量为m的小球,现将小球拉至悬线水平位置后由静止释放,如图所示,试求在小球摆动过程中,小车的最大速度和最大位移.