题目内容
2. 质量为M的带支架的小车静止在光滑水平地面上,支架上用长为L的轻绳悬挂一质量为m的小球,现将小球拉至悬线水平位置后由静止释放,如图所示,试求在小球摆动过程中,小车的最大速度和最大位移.
质量为M的带支架的小车静止在光滑水平地面上,支架上用长为L的轻绳悬挂一质量为m的小球,现将小球拉至悬线水平位置后由静止释放,如图所示,试求在小球摆动过程中,小车的最大速度和最大位移.
分析 小球从静止下摆时,系统水平方向不受外力,水平方向动量守恒.小球下摆到最低点时,小车的速度最大.根据系统的水平方向动量守恒和机械能守恒列式,即可求出小车的最大速度.
根据系统水平方向平均动量守恒,用水平位移表示小球和小车的速度,根据动量守恒列式求解小车向右移动的最大位移.
解答 解:当小球摆至最低点时,小球和小车的速度大小分别为v1和v2.取水平向左为正方向,据系统水平方向动量守恒得:
mv1-Mv2=0
另据系统的机械能守恒得:mgL=$\frac{1}{2}$mv12+$\frac{1}{2}$Mv22
得小车的最大速度 v2=$\frac{m}{M}$$\sqrt{\frac{2MgR}{M+m}}$
当小球从开始到摆到最低点的过程中,小球水平位移的大小为s1,小车水平位移的大小为s2.
在这一过程中,由系统水平方向总动量守恒得(取水平向左为正方向)
m$\frac{{s}_{1}}{t}$-M$\frac{{s}_{2}}{t}$=0
又 s1+s2=L
由此可得:s2=$\frac{mL}{M+m}$
所以小车的最大位移为:sm=2s2=$\frac{2mL}{M+m}$
答:小车的最大速度为$\frac{m}{M}$$\sqrt{\frac{2MgR}{M+m}}$,最大位移为$\frac{2mL}{M+m}$.
点评 本题中前两题是常规题,利用系统水平方向动量守恒和机械能守恒列式,即可求出相关量.

练习册系列答案
相关题目
13. 如图所示为改进后的回旋加速器的示意图,其中距离很小的盒缝间的加速电场的场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向进入加速电场,经加速后进入D形盒中的匀强磁场做匀速圆周运动,对于这种回旋加速器,下列说法正确的是( )
如图所示为改进后的回旋加速器的示意图,其中距离很小的盒缝间的加速电场的场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向进入加速电场,经加速后进入D形盒中的匀强磁场做匀速圆周运动,对于这种回旋加速器,下列说法正确的是( )
 如图所示为改进后的回旋加速器的示意图,其中距离很小的盒缝间的加速电场的场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向进入加速电场,经加速后进入D形盒中的匀强磁场做匀速圆周运动,对于这种回旋加速器,下列说法正确的是( )
如图所示为改进后的回旋加速器的示意图,其中距离很小的盒缝间的加速电场的场强大小恒定,且被限制在A、C板间,带电粒子从P0处静止释放,并沿电场线方向进入加速电场,经加速后进入D形盒中的匀强磁场做匀速圆周运动,对于这种回旋加速器,下列说法正确的是( )| A. | 带电粒子每运动一周被加速一次 | |
| B. | P1P2=P2P3 | |
| C. | 粒子能达到的最大速度与D形盒的尺寸无关 | |
| D. | 加速电场的方向需要做周期性的变化 |
17.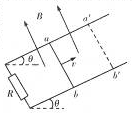 如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )
如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )
 如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )
如图所示,电阻不计的平行光滑金属导轨与水平面的夹角为θ,宽度为L,下端与阻值为R的电阻相连.磁感应强度为B的匀强磁场垂直穿过导轨平面,现使质量为m的导体棒ab位置以平行于斜面的初速度沿导轨向上运动,滑行到最远位置a′b′后又下滑.已知导体棒运动过程中的最大加速度为2gsinθ,g为重力加速度,轨道足够长,则( )| A. | 导体棒运动过程中的最大速度$\frac{mgsinθ}{{B}^{2}{l}^{2}}$ | |
| B. | R上的最大热功率为$\frac{{{m^2}{g^2}R{{sin}^2}θ}}{{{B^2}{l^2}}}$ | |
| C. | 导体棒返回到ab位置前已经达到下滑的最大速度 | |
| D. | 导体棒返回到ab位置时刚好达到下滑的最大速度 |
7. 如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段,则下列说法中正确的是( )
如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段,则下列说法中正确的是( )
 如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段,则下列说法中正确的是( )
如图所示,物体的运动分三段,第1、2s为第Ⅰ段,第3、4s为第Ⅱ段,第5s为第Ⅲ段,则下列说法中正确的是( )| A. | 第Ⅰ段与第Ⅲ段平均速度不相等 | |
| B. | 第1s内的加速度小于第5s内的加速度 | |
| C. | 第1s末与第4.5s末的速度方向相同 | |
| D. | 第Ⅲ段的加速度与速度的方向不同 |
14.质量为m的汽车以恒定功率P沿倾角为θ的倾斜路面向上行驶,最终以速度v匀速运动,若保持汽车的功率P不变,使汽车沿这个倾斜路面向下运动,最后匀速行驶,由此可知(汽车所受阻力大小不变)( )
| A. | 汽车的最后速度一定大于v | B. | 汽车的最后速度可能小于v | ||
| C. | 汽车所受的阻力一定大于mgsinθ | D. | 汽车所受的阻力可能小于mgsinθ |
 某实验探究小组为了测定滑动变阻器上金属丝的电阻率,除待测滑动变阻器Rx(总阻值约25Ω)外,在实验室还找到了下列器材.
某实验探究小组为了测定滑动变阻器上金属丝的电阻率,除待测滑动变阻器Rx(总阻值约25Ω)外,在实验室还找到了下列器材. 用F=50N的力拉一个物体在水平面上做匀速运动,F的方向与水平面的夹角为37°,物体的质量为10kg,若物体前进了10m,拉力F做的功为400J,重力做的功为0J,支持力做的功为0J,摩擦力做的功为-400J.
用F=50N的力拉一个物体在水平面上做匀速运动,F的方向与水平面的夹角为37°,物体的质量为10kg,若物体前进了10m,拉力F做的功为400J,重力做的功为0J,支持力做的功为0J,摩擦力做的功为-400J.