题目内容
18. 如图所示,水平的粗糙轨道与竖直的光滑圆形轨道相连,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续沿水平轨道运动.圆形轨道半径R=0.2m,右侧水平轨道BC长为L=4m,C点右侧有一壕沟,C、D两点的竖直高度h=1m,水平距离s=2m,小球与水平轨道间的动摩擦因数μ=0.2,重力加速度g=10m/s2.小球从圆形轨道最低点B以某一水平向右的初速度出发,进入圆形轨道.试求:
如图所示,水平的粗糙轨道与竖直的光滑圆形轨道相连,圆形轨道间不相互重叠,即小球离开圆形轨道后可继续沿水平轨道运动.圆形轨道半径R=0.2m,右侧水平轨道BC长为L=4m,C点右侧有一壕沟,C、D两点的竖直高度h=1m,水平距离s=2m,小球与水平轨道间的动摩擦因数μ=0.2,重力加速度g=10m/s2.小球从圆形轨道最低点B以某一水平向右的初速度出发,进入圆形轨道.试求:(1)若小球通过圆形轨道最高点A时给轨道的压力大小恰为小球的重力大小,求小球在B点的初速度多大?
(2)小球在上述(1)的运动中,最后停在距离B点为d的E点(图中未画出),求距离d的大小;
(3)若小球从B点向右出发,在以后的运动过程中,小球既不脱离圆形轨道,又不掉进壕沟,求小球在B点的初速度大小的范围.
分析 (1)小球恰好通过最高点,则重力充当向心力;再对B到最高点过程,由机械能守恒定律可求得B点的速度.
(2)从B到E运用动能定理,即可求出距离d的大小;
(3)小球飞出后做平抛运动,由平抛运动的规律可求得小球在B点的初速度范围
解答 解:(1)小球在最高点A处,由牛顿第三定律可知轨道对小球的压力:FN=FN′=mg
由牛顿第二定律得:FN+mg=m$\frac{{v}_{A}^{2}}{R}$
从B到A过程,由动能定理可得:-mg•2R=$\frac{1}{2}$mvA2-$\frac{1}{2}$mv02
联立解得:v0=2$\sqrt{3}$m/s
(2)根据动能定理可得:-μmgd=0-$\frac{1}{2}m{v}_{0}^{2}$
解得:d=3m
(3)情况一:若小球恰好停在C处,对全程进行研究,由动能定理得:-μmgL=0-$\frac{1}{2}$mv12
代入数据解得:v1=4m/s
若小球恰好过最高点A,由牛顿第二定律得:mg=m$\frac{v{′}_{A}^{2}}{R}$
从B到A过程,由动能定理得:-mg•2R=$\frac{1}{2}$mvA′2-$\frac{1}{2}$mv22
解得:v2=$\sqrt{10}$m/s
所以当$\sqrt{10}$m/s≤vB≤4m/s时,小球停在BC间
情况二:若小球恰能越过壕沟,由动能定理得:-μmgL=$\frac{1}{2}$mvC2-$\frac{1}{2}$mv32
小球做平抛运动:h=$\frac{1}{2}$gt2
s=vCt
解得:v3=6m/s
所以当vB≥6m/s时,小球越过壕沟
情况三:若小球刚好能运动到与圆心等高位置,则有:-mgR=0-$\frac{1}{2}$mv42
解得:v4=2m/s
所以当vB≤2m/s时,小球又沿圆轨道返回
综上所述,小球在A点的初速度的范围是vB≤2m/s 或$\sqrt{10}$m/s≤vB≤4m/s、或vB≥6m/s;
答:(1)小球在B点的初速度是2$\sqrt{3}$m/s;
(2)距离d的大小为3m;
(3)小球在B点的初速度的范围是:vB≤2m/s 或$\sqrt{10}$m/s≤vB≤4m/s、或vB≥6m/s;.
点评 本题考查动能定理、平抛运动及圆周运动中的向心力公式,在解题时要注意正确分析物理过程,做好受力分析,再选择合适的物理规律求解即可;注意分析临界状态,把握临界条件是重点.

| A. | 贝克勒尔通过α粒子轰击铍核的实验,发现了中子的存在 | |
| B. | 卢瑟福发现了电子并提出了原子结构的“枣糕”模型 | |
| C. | 利用玻尔理论可以准确计算出氦原子发光时放出的可见光的频率 | |
| D. | β衰变的本质是原子核内的一个中子释放一个电子变为质子 |

| A. | 小物体与甲传送带间的动摩擦因数较小 | |
| B. | 两传送带对小物体做功不相等 | |
| C. | 甲传送带消耗的电能比较大 | |
| D. | 两种情况下因摩擦产生的热量不相等 |
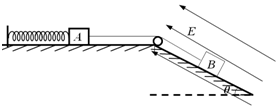 如图所示,物体A和带负电的物体B用跨过定滑轮的绝缘轻绳连接,A、B的质量分别是m和2m,劲度系数为k的轻质弹簧一端固定在水平面上,另一端与物体A相连,倾角为θ的斜面处于沿斜面向上的匀强电场中,整个系统不计一切摩擦.开始时,物体B在一沿斜面向上的外力F=3mgsinθ的作用下保持静止且轻绳恰好伸直,然后撤去外力F,直到物体B获得最大速度,且弹簧未超过弹性限度,则在此过程中( )
如图所示,物体A和带负电的物体B用跨过定滑轮的绝缘轻绳连接,A、B的质量分别是m和2m,劲度系数为k的轻质弹簧一端固定在水平面上,另一端与物体A相连,倾角为θ的斜面处于沿斜面向上的匀强电场中,整个系统不计一切摩擦.开始时,物体B在一沿斜面向上的外力F=3mgsinθ的作用下保持静止且轻绳恰好伸直,然后撤去外力F,直到物体B获得最大速度,且弹簧未超过弹性限度,则在此过程中( )| A. | 撤去外力F的瞬间,物体A的加速度为gsinθ | |
| B. | 撤去外力F的瞬间,物体B的加速度为$\frac{3gsinθ}{2}$ | |
| C. | A、B获得最大速度时,弹簧伸长量为 $\frac{3mgsinθ}{k}$ | |
| D. | 物体A和弹簧组成的系统机械能守恒 |
| A. | 线速度 | B. | 角速度 | C. | 向心加速度 | D. | 向心力 |
 如图,某物体在四个共点力作用下处于平衡状态,若将F4=5N的力沿逆时针方向转动90°,其余三个力的大小和方向不变,则此时物体所受合力的大小为( )
如图,某物体在四个共点力作用下处于平衡状态,若将F4=5N的力沿逆时针方向转动90°,其余三个力的大小和方向不变,则此时物体所受合力的大小为( )| A. | 0 | B. | 10N | C. | 5N | D. | 5$\sqrt{2}$N |
 一个质量m=1.7×10-27kg,电荷量q=1.6×10-19C的正离子,以速度v=6.4×106m/s垂直于屏并经过小孔O射入存在着匀强磁场的真空中,如图所示,磁感应强度B的方向与离子的入射速度方向垂直,并垂直于纸面向里,磁感应强度的大小B=0.17T,求:
一个质量m=1.7×10-27kg,电荷量q=1.6×10-19C的正离子,以速度v=6.4×106m/s垂直于屏并经过小孔O射入存在着匀强磁场的真空中,如图所示,磁感应强度B的方向与离子的入射速度方向垂直,并垂直于纸面向里,磁感应强度的大小B=0.17T,求: 如图所示,在某竖直平面内,光滑曲面AB与水平面BC平滑连接于B点,BC右端连接一口深为H,宽度为d的深井CDEF,一个质量为m的小球放在曲面AB上,可从距BC面不同的高度处静止释放小球,已知BC段长L,小球与BC间的动摩擦因数为μ,取重力加速度g=10m/s2,则:
如图所示,在某竖直平面内,光滑曲面AB与水平面BC平滑连接于B点,BC右端连接一口深为H,宽度为d的深井CDEF,一个质量为m的小球放在曲面AB上,可从距BC面不同的高度处静止释放小球,已知BC段长L,小球与BC间的动摩擦因数为μ,取重力加速度g=10m/s2,则: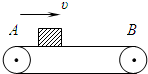 如图所示,水平传送带以v=2m/s的速度匀速运动,A、B两点相距s=11m,一质量m=1kg的物块(可视为质点)从A点由静止开始运动.已知物块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2.
如图所示,水平传送带以v=2m/s的速度匀速运动,A、B两点相距s=11m,一质量m=1kg的物块(可视为质点)从A点由静止开始运动.已知物块与传送带间的动摩擦因数μ=0.2,重力加速度g=10m/s2.