题目内容
12. 如图所示,一轻质弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然伸长状态.直轨道与一半径为R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R.已知P与直轨道间的动摩擦因数μ=0.25,重力加速度大小为g.(取sin37°=0.6,cos37°=0.8)
如图所示,一轻质弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然伸长状态.直轨道与一半径为R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R.已知P与直轨道间的动摩擦因数μ=0.25,重力加速度大小为g.(取sin37°=0.6,cos37°=0.8)(1)求P第一次运动到B点时速度的大小;
(2)求P运动到E点时弹簧的弹性势能;
(3)改变物块P的质量,将P推至E点,从静止开始释放.P到达圆轨道最高点D时对轨道的压力为重力的0.2倍,求P运动到D点时速度的大小和改变后小物块P的质量.
分析 (1)对C到B的过程应用动能定理即可求解;
(2)对C到E和E到F的运动过程分别应用动能定理,即可联立求解;
(3)由牛顿第三定律求得P在D处受到的支持力,然后由牛顿第二定律求得速度,即可由动能定理求解.
解答 解:(1)P从C到B的过程作用重力、摩擦力做功,故由动能定理可得:$mgBCsin37°-μmgBCcos37°=\frac{1}{2}m{{v}_{B}}^{2}-0$,所以,${v}_{B}=\sqrt{2gBC(sin37°-μcos37°)}=2\sqrt{gR}$;
(2)设AE=x,那么CE=7R-x,EF=4R-x;
对滑块从C到E应用动能定理可得:mgCEsin37°-μmgCEcos37°-Ep=0,所以,Ep=0.4mgCE=0.4mg(7R-x);
对滑块从E到F应用动能定理可得:Ep-mgEFsin37°-μmgEFcos37°=0,所以,Ep=0.8mgEF=0.8mg(4R-x);
所以,x=R,Ep=2.4mgR;
(3)P到达圆轨道最高点D时对轨道的压力为重力的0.2倍,那么由牛顿第三定律可得:P受到轨道的作用力FN=0.2m′g,方向竖直向下;
在最高点D,由牛顿第二定律可得:${F}_{N}+m′g=\frac{m′{{v}_{D}}^{2}}{R}$,所以,${v}_{D}=\sqrt{1.2gR}$;
对P从E到D的运动过程应用动能定理可得:${E}_{p}-m′g(CEsin37°+Rcos37°+R)-μm′gCEcos37°=\frac{1}{2}m′{{v}_{D}}^{2}=0.6m′gR$;
所以,2.4mgR-5.4m′gR-1.2m′gR=0.6m′gR,所以,$m′=\frac{1}{3}m$;
答:(1)P第一次运动到B点时速度的大小为$2\sqrt{gR}$;
(2)P运动到E点时弹簧的弹性势能为2.4mgR;
(3)改变物块P的质量,将P推至E点,从静止开始释放.P到达圆轨道最高点D时对轨道的压力为重力的0.2倍,则P运动到D点时速度的大小为$\sqrt{1.2gR}$;改变后小物块P的质量为$\frac{1}{3}m$.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.

 如图所示,起重机匀速吊起物体的过程中,钢索对物体的拉力F做正(填“正”或“负”)功;重力G对物体做负(填“正”或“负”)功;拉力F的瞬时功率不变(填“变大”.
如图所示,起重机匀速吊起物体的过程中,钢索对物体的拉力F做正(填“正”或“负”)功;重力G对物体做负(填“正”或“负”)功;拉力F的瞬时功率不变(填“变大”.



 如图所示,在双缝干涉实验中,S1和S2为双缝,P是光屏上的一点,已知P点与S1、S2距离之差为2.1×10-6m,用单色光B在空气中做双缝干涉实验.已知B光在某种介质中波长为λ=3.15×10-7m,当B光从这种介质射向空气时,临界角为37°.已知sin37°=0.6.
如图所示,在双缝干涉实验中,S1和S2为双缝,P是光屏上的一点,已知P点与S1、S2距离之差为2.1×10-6m,用单色光B在空气中做双缝干涉实验.已知B光在某种介质中波长为λ=3.15×10-7m,当B光从这种介质射向空气时,临界角为37°.已知sin37°=0.6. 如图为火车站装载货物的示意图,AB段是距水平传送带装置高为H=5m的光滑斜面,水平段BC使用水平传送带装置,BC长L=8m,与货物包的摩擦系数为μ=0.6,皮带轮的半径为R=0.2m,上部距车厢底水平面的高度h=0.45m.设货物由静止开始从A点下滑,经过B点的拐角处无能量损失.通过调整皮带轮(不打滑)的转动角速度ω可使货物经C点被水平抛出后落在车厢上的不同位置(车厢足够长,货物不会撞到车厢壁),取g=10m/s2.
如图为火车站装载货物的示意图,AB段是距水平传送带装置高为H=5m的光滑斜面,水平段BC使用水平传送带装置,BC长L=8m,与货物包的摩擦系数为μ=0.6,皮带轮的半径为R=0.2m,上部距车厢底水平面的高度h=0.45m.设货物由静止开始从A点下滑,经过B点的拐角处无能量损失.通过调整皮带轮(不打滑)的转动角速度ω可使货物经C点被水平抛出后落在车厢上的不同位置(车厢足够长,货物不会撞到车厢壁),取g=10m/s2.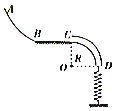 如图所示,水平地面BC与光滑曲面AB相切于B点,与内壁光滑的$\frac{1}{4}$细圆管CD相切于C点,管口D正下方直立一劲度系数为k的轻弹簧,弹簧下端固定,上端恰好与管口D齐平.将质量为m的小物块(可视为质点)放在弹簧上端且缓慢下压弹簧,当弹簧压缩的长度x1=$\frac{4mg}{k}$(其中g为重力加速度大小),对应弹簧的弹性势能Ep1=$\frac{8{m}^{2}{g}^{2}}{k}$时,由静止开始释放物块,物块进入管口D后沿DCBA轨道运动且不脱离轨道.已知物块速度最大时弹性势能Ep2=$\frac{{m}^{2}{g}^{2}}{2k}$,物块与BC间的动摩擦因数μ=0.8,BC的长度L1=$\frac{mg}{k}$,圆管CD的半径R=$\frac{mg}{k}$,求:
如图所示,水平地面BC与光滑曲面AB相切于B点,与内壁光滑的$\frac{1}{4}$细圆管CD相切于C点,管口D正下方直立一劲度系数为k的轻弹簧,弹簧下端固定,上端恰好与管口D齐平.将质量为m的小物块(可视为质点)放在弹簧上端且缓慢下压弹簧,当弹簧压缩的长度x1=$\frac{4mg}{k}$(其中g为重力加速度大小),对应弹簧的弹性势能Ep1=$\frac{8{m}^{2}{g}^{2}}{k}$时,由静止开始释放物块,物块进入管口D后沿DCBA轨道运动且不脱离轨道.已知物块速度最大时弹性势能Ep2=$\frac{{m}^{2}{g}^{2}}{2k}$,物块与BC间的动摩擦因数μ=0.8,BC的长度L1=$\frac{mg}{k}$,圆管CD的半径R=$\frac{mg}{k}$,求:
 质量为m的物体从高出地面H处由静止开始自由落下,不考虑空气阻力,落至地面进入沙坑h米停止,求物体在沙坑中受到的平均阻力.
质量为m的物体从高出地面H处由静止开始自由落下,不考虑空气阻力,落至地面进入沙坑h米停止,求物体在沙坑中受到的平均阻力. 动车组列车是由几节自带动力的车厢(动车)和几节不带动力的车厢(拖车)编成一组.某兴趣小组在模拟实验中用4节小动车和4节小拖车组成动车组,总质量为m=2kg,每节动车可以提供P0=3W的额定功率.开始时动车组先以恒定加速度a=1m/s2启动做匀加速直线运动,达到额定功率后保持功率不变再做变加速直线运动,直至动车组达到最大速度vm=6m/s并开始匀速行驶.行驶过程中所受阻力恒定.
动车组列车是由几节自带动力的车厢(动车)和几节不带动力的车厢(拖车)编成一组.某兴趣小组在模拟实验中用4节小动车和4节小拖车组成动车组,总质量为m=2kg,每节动车可以提供P0=3W的额定功率.开始时动车组先以恒定加速度a=1m/s2启动做匀加速直线运动,达到额定功率后保持功率不变再做变加速直线运动,直至动车组达到最大速度vm=6m/s并开始匀速行驶.行驶过程中所受阻力恒定.