题目内容
3. 半径为R的透明圆柱体,过其轴线OO′的截面如图所示,位于截面所在平面内的一细束光线,以角i0=60°由O点入射,折射光线由上边界的A点射出,A点与左端面的距离为R,当光线在O点的入射角减小至某一值时,折射光线在上边界的B点恰好发生全反射.求B点与左端间的距离.
半径为R的透明圆柱体,过其轴线OO′的截面如图所示,位于截面所在平面内的一细束光线,以角i0=60°由O点入射,折射光线由上边界的A点射出,A点与左端面的距离为R,当光线在O点的入射角减小至某一值时,折射光线在上边界的B点恰好发生全反射.求B点与左端间的距离.
分析 由折射定律求出光线在左侧面上的折射角,可几何关系求出光线在A点的入射角,并求得光线在O点的折射角,即可求得折射率.由sinC=$\frac{1}{n}$求出全反射临界角C,再由几何知识求解B与左端间的距离.
解答  解:设当光线在O点的入射角为i0时,折射角为r0,如图所示,由题,AD=DO=R,则 r0=45°
解:设当光线在O点的入射角为i0时,折射角为r0,如图所示,由题,AD=DO=R,则 r0=45°
由折射定律得:$\frac{sin{i}_{0}}{sin{r}_{0}}$=n
可得:n=$\frac{\sqrt{6}}{2}$
若光线在B点恰好发生全反射,则在B点的入射角恰好等于临界角C,设B点与左端间的距离BD=d.则有:
sinC=$\frac{1}{n}$
由几何关系得:sinC=$\frac{d}{\sqrt{{d}^{2}{+R}^{2}}}$
联立解得:d=$\sqrt{2}$R
答:B点与左端间的距离为$\sqrt{2}$R.
点评 解决本题的关键要作出光路图,明确全反射的条件,运用几何知识和折射定律结合解答.

练习册系列答案
相关题目
11.下列说法符合事实的是( )
| A. | 光电效应说明了光具有波动性 | |
| B. | 查德威克用α粒子轰击氮14获得反冲核氧18,发现了中子 | |
| C. | 贝克勒尔发现的天然放射性现象,说明原子核有复杂结构 | |
| D. | 汤姆生通过对阴极射线的研究,提出了原子核式结构模型 |
18. 如图所示,甲、乙为竖直平面内两光滑的固定半圆形轨道,轨道甲的半径小于轨道乙,两轨道的圆心等高.a、b为两可视为质点的小球,a球质量大于b球质量.现让两球分别从轨道左端最高点由静止释放,在各自到达轨道最低点时,有( )
如图所示,甲、乙为竖直平面内两光滑的固定半圆形轨道,轨道甲的半径小于轨道乙,两轨道的圆心等高.a、b为两可视为质点的小球,a球质量大于b球质量.现让两球分别从轨道左端最高点由静止释放,在各自到达轨道最低点时,有( )
 如图所示,甲、乙为竖直平面内两光滑的固定半圆形轨道,轨道甲的半径小于轨道乙,两轨道的圆心等高.a、b为两可视为质点的小球,a球质量大于b球质量.现让两球分别从轨道左端最高点由静止释放,在各自到达轨道最低点时,有( )
如图所示,甲、乙为竖直平面内两光滑的固定半圆形轨道,轨道甲的半径小于轨道乙,两轨道的圆心等高.a、b为两可视为质点的小球,a球质量大于b球质量.现让两球分别从轨道左端最高点由静止释放,在各自到达轨道最低点时,有( )| A. | a 球的速度一定大于 b 球的速度 | |
| B. | a 球的动能一定小于 b 球的动能 | |
| C. | a 球的向心加速度一定小于 b 球的向心加速度 | |
| D. | a 球对轨道的压力一定大于 b 球对轨道的压力 |
8.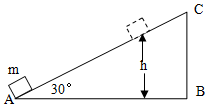 如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{2}{3}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{2}{3}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
 如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{2}{3}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{2}{3}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了mgh | B. | 动能损失了$\frac{4}{3}$mgh | ||
| C. | 克服摩擦力做功$\frac{1}{6}$mgh | D. | 机械能损失了$\frac{1}{2}$mgh |
12. 如图所示,高为h的光滑斜面体abc固定在水平地面上,其中a、b分别为斜面的顶端与低端,将一质量为m的小球从a点由静止释放,取地面为零势能面,重力加速度其g,一下说法正确的是( )
如图所示,高为h的光滑斜面体abc固定在水平地面上,其中a、b分别为斜面的顶端与低端,将一质量为m的小球从a点由静止释放,取地面为零势能面,重力加速度其g,一下说法正确的是( )
 如图所示,高为h的光滑斜面体abc固定在水平地面上,其中a、b分别为斜面的顶端与低端,将一质量为m的小球从a点由静止释放,取地面为零势能面,重力加速度其g,一下说法正确的是( )
如图所示,高为h的光滑斜面体abc固定在水平地面上,其中a、b分别为斜面的顶端与低端,将一质量为m的小球从a点由静止释放,取地面为零势能面,重力加速度其g,一下说法正确的是( )| A. | 小球在a点时的重力势能为mgh | B. | 小球在b点时的重力势能为mgh | ||
| C. | 小球在a点时的机械能为mgh | D. | 小球在b点时的机械能为mgh |
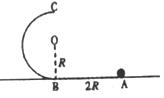 如图,在竖直平面内有一固定的光滑轨道ABC,其中AB是长为2R的水平直轨道,BC是圆心为O、半径为R的半圆弧轨道,两轨道相切于B点.在水平向左的恒定拉力F作用下,一质量为m的小球从A点由静止开始做匀加速直线运动,到达B点时撤除拉力.已知小球经过最高点C时对轨道的压力大小恰好等于小球的重力大小,已知重力加速度大小为g.求:
如图,在竖直平面内有一固定的光滑轨道ABC,其中AB是长为2R的水平直轨道,BC是圆心为O、半径为R的半圆弧轨道,两轨道相切于B点.在水平向左的恒定拉力F作用下,一质量为m的小球从A点由静止开始做匀加速直线运动,到达B点时撤除拉力.已知小球经过最高点C时对轨道的压力大小恰好等于小球的重力大小,已知重力加速度大小为g.求: 如图所示,一轻弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然状态,直轨道与一半径为$\frac{5}{6}$R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R,已知P与直轨道间的动摩擦因数?=$\frac{1}{4}$,重力加速度为g,sin37°=0.6,cos37°=0.8.则:
如图所示,一轻弹簧原长为2R,其一端固定在倾角为370的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然状态,直轨道与一半径为$\frac{5}{6}$R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直平面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高到达F点,AF=4R,已知P与直轨道间的动摩擦因数?=$\frac{1}{4}$,重力加速度为g,sin37°=0.6,cos37°=0.8.则: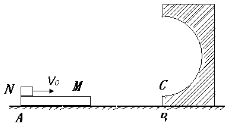 如图所示,质量为1Kg的小滑块N(可视为质点)放在质量也为1Kg的长木板M左端,N和M之间的动摩擦因数μ1=0.5,M和地面之间的动摩擦因数μ2=0.1,现给小滑块N一个水平向右的初速v0=8m/s,小滑块N和长木板M同时到达B点且此时速度大小恰好相等,小滑块到达长木板右端后,能够由C点平滑地滑上固定的光滑圆弧轨道,圆轨道半径R=0.3m,重力加速度g取10m/s2,求:
如图所示,质量为1Kg的小滑块N(可视为质点)放在质量也为1Kg的长木板M左端,N和M之间的动摩擦因数μ1=0.5,M和地面之间的动摩擦因数μ2=0.1,现给小滑块N一个水平向右的初速v0=8m/s,小滑块N和长木板M同时到达B点且此时速度大小恰好相等,小滑块到达长木板右端后,能够由C点平滑地滑上固定的光滑圆弧轨道,圆轨道半径R=0.3m,重力加速度g取10m/s2,求: