题目内容
15．古时有“守株待兔”的寓言，假设兔子质量约为2kg，以5m/s的速度奔跑，撞树后经0.2s反弹，反弹的速度为2m/s，则兔子受到撞击力的冲大小为 （ ）| A． | 7N | B． | 14N | C． | 28N | D． | 70N |
分析 由题意可知初速度、末速度，则直接由动量定理可求得冲量的大小．
解答 解：设初速度方向为正方向，则由题意可知，初速度为：v0=5m/s
末速度为：v=-2m/s；
则由动量定理可知：I=mv-mv0=-2×2-2×5=-14N•s；
又：I=Ft
所以：F=$\frac{I}{t}=\frac{14}{0.2}=70$N．故ABC错误，D正确
故选：D．
点评 本题考查动量定理的直接应用，同于表达式中有多个矢量，故应注意设定正方向，并明确各量的方向．
练习册系列答案
名校课堂系列答案
相关题目
节水喷灌示意图如图所示，喷口距地面h高，将水水平喷出，其喷灌半径可达8h，时间t内喷出水的质量为m，所用的水是水泵从地下3h深的井里抽取．设水以相同的速率从喷口喷出，水泵效率为η，不计空气阻力，试求：
6．下列说法中正确的是（ ）
| A． | 开普勒发现了万有引力定律 | |
| B． | 牛顿测出了万有引力常量 | |
| C． | 牛顿发现了万有引力定律，卡文迪许测出了万有引力常量 | |
| D． | 伽利略提出所有行星绕太阳运动的轨道都是椭圆 |
半径为R的透明圆柱体，过其轴线OO′的截面如图所示，位于截面所在平面内的一细束光线，以角i0=60°由O点入射，折射光线由上边界的A点射出，A点与左端面的距离为R，当光线在O点的入射角减小至某一值时，折射光线在上边界的B点恰好发生全反射．求B点与左端间的距离．
宇航员在太空站内做了如下实验：选取两个质量分别为mA=0.2kg、mB=0.4kg的小球A、B和一根轻质短弹簧，弹簧的一端与小球A粘连，另一端与小球B接触而不粘连．现使小球A和B之间夹着被压缩的轻质弹簧，处于锁定状态，一起以速度v0=0.1m/s做匀速直线运动，如图所示，过一段时间，突然解除锁定（解除锁定没有机械能损失），两球仍沿原直线运动，从弹簧与小球B刚刚分离开始计时，经时间t=3.0s，两球之间的距离增加了S=2.7m，求弹簧被锁定时的弹性势能Ep．
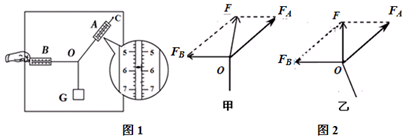
20．在一光滑水平面内建立平面直角坐标系，一物体从t=0时刻起，由坐标原点O（0，0）开始运动，其沿x轴和y轴方向运动的速度-时间图象如图甲、乙所示，下列说法中正确的是（ ）
| A． | 前2s内物体做匀加速直线运动，加速度沿x轴方向 | |
| B． | 后2s内物体继续做匀加速直线运动，但加速度沿y轴方向 | |
| C． | 4s 末物体坐标为（4 m，4 m） | |
| D． | 4 s末物体坐标为（6m，2m） |
7．水平传送带匀速运动，速度大小为v，现将一小工件放到传送带上．该工件初速度为零，当它在传送带上滑动一段距离后速度达到v后与传送带保持相对静止．设工件质量为m，它与传送带间的滑动摩擦系数为μ，则在工件相对传送带滑动的过程中下列说法正确的是（ ）
| A． | 摩擦力对工件做的功为$\frac{1}{2}$mv2 | |
| B． | 系统增加的内能为$\frac{1}{2}$mv2 | |
| C． | 传送带需额外做的功为$\frac{1}{2}$mv2 | |
| D． | 工件相对于传送带滑动的路程大小为$\frac{{v}^{2}}{2μg}$ |
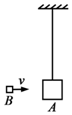如图，物块A通过一不可伸长的轻绳悬挂在天花板下，初始时静止．从发射器（图中未画出）射出的物块B沿水平方向与A相撞，碰撞前B的速度大小为v，碰撞后两者粘连在一起运动．已知A和B的质量分别M和m，重力加速度大小为g，不计空气阻力，求：