题目内容
14. 如图所示,长为L的绳子(不可伸长,质量不计),一端固定于O点,另一端系着质量为m的小球.在O点正下方距离为$\frac{4}{5}$L处钉有一颗钉子,现将悬线沿水平方向拉直无初速度释放,悬线碰到钉子后,小球做完整圆周运动,则小球到达圆周运动最高点时,速度大小为$\sqrt{\frac{6}{5}gL}$,绳子对小球拉力大小为5mg.
如图所示,长为L的绳子(不可伸长,质量不计),一端固定于O点,另一端系着质量为m的小球.在O点正下方距离为$\frac{4}{5}$L处钉有一颗钉子,现将悬线沿水平方向拉直无初速度释放,悬线碰到钉子后,小球做完整圆周运动,则小球到达圆周运动最高点时,速度大小为$\sqrt{\frac{6}{5}gL}$,绳子对小球拉力大小为5mg.
分析 根据动能定理求出小球到达最高点时的速度,再在最高点,根据向心力公式列式求解绳子拉力大小.
解答 解:从释放到运动到最高点的过程中,根据动能定理得:
$\frac{1}{2}m{v}^{2}=mg(L-2×\frac{1}{5}L)$
解得:v=$\sqrt{\frac{6}{5}gL}$
在最高点,根据向心力公式得:
T+mg=m$\frac{{v}^{2}}{\frac{L}{5}}$
解得:T=5mg
故答案为:$\sqrt{\frac{6}{5}gL}$;5mg
点评 本题主要考查了动能定理及向心力公式的直接应用,知道竖直平面内的圆周运动,在最高点和最低点是由合外力提供向心力,难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知存在以下几种使物体带电的办法:
①摩擦起电;②接触起电;③静电感应;④电介质的极化
其中前三种方式是同学们熟悉的,对第④种方式的简介如下、一些电介质(绝缘体)的分子在受到外电场的作用时,在跟外电场垂直的两个表面上会出现等量的正、负电荷,这种电荷不能离开电介质,也不能在电介质内部自由移动,叫做束缚电荷.
用丝绸摩擦过的玻璃棒去靠近碎纸屑,对于可能出现的情况及其分析,下列选项中正确的是( )
①摩擦起电;②接触起电;③静电感应;④电介质的极化
其中前三种方式是同学们熟悉的,对第④种方式的简介如下、一些电介质(绝缘体)的分子在受到外电场的作用时,在跟外电场垂直的两个表面上会出现等量的正、负电荷,这种电荷不能离开电介质,也不能在电介质内部自由移动,叫做束缚电荷.
用丝绸摩擦过的玻璃棒去靠近碎纸屑,对于可能出现的情况及其分析,下列选项中正确的是( )
| A. | 玻璃棒会吸引纸屑,这是因为纸屑通过第①种方式带了电 | |
| B. | 有些纸屑会粘在玻璃棒上,这是因为纸屑通过第④种方式带了电 | |
| C. | 有些纸屑被玻璃棒吸引,吸上后又马上弹开,整个过程只包含第②种带电方式 | |
| D. | 有些纸屑被玻璃棒吸引,吸上后又马上弹开,整个过程包括第②和第③两种带电方式 |
5.如图所示,等腰直角三角形的ABC为棱镜截面,∠A=90°,一束由两种单色光a,b组成的复色光平行于BC边射入棱镜,经过AB折射后光线射到BC边上,则以下说法正确的是( )

| A. | 光线a在BC边一定能发生全反射,b光不能发生全反射 | |
| B. | a,b光一定能从AC边射出,并且出射光线一定与入射光线平行 | |
| C. | a,b光在AC边射出后光线又变为一束 | |
| D. | 用a,b光做双缝干涉实验时,a光得到的亮条纹更宽 |
9.关于经典力学的发展历程和取得成就的表述,不正确的是( )
| A. | 哥白尼最早创立了日心说,将人们的思想从中世纪的愚昧中解放出来 | |
| B. | 伽利略发展了观察与实验法、科学思维与数学相结合的物理学研究方法 | |
| C. | 牛顿在总结前人研究的基础上,发现了牛顿运动定律及万有引力定律 | |
| D. | 经典力学认为天体运动和地面上宏观物体的运动,分别遵循不同的运动规律 |
19.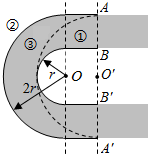 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )
如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O点的半圆,内外半径分别为r和2r,一辆质量为m的赛车通过AB线经弯道到达A′B′线,有如图所示的①、②、③三条路线,其中路线③是以O′为圆心的半圆,OO′=r,赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为Fmax,选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )| A. | 选择路线①,赛车经过的路程最短 | |
| B. | 选择路线②,赛车的速率最小 | |
| C. | 选择路线③,赛车所用时间最短 | |
| D. | ①、②、③三条路线的圆弧上,赛车的向心加速度大小相等 |

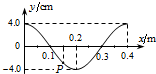 图示为xoy平面内沿x轴传播的简谐横波在t0=0时刻的波形图象,其波速v=5.0m/s.此时平衡位置xp=0.15m的P点正在向-y方向运动,则该波的传播方向是-x(选填“+x”或“-x”),经过△t=0.05s时间P点的加速度第一次达到最大且指向y轴负方向.
图示为xoy平面内沿x轴传播的简谐横波在t0=0时刻的波形图象,其波速v=5.0m/s.此时平衡位置xp=0.15m的P点正在向-y方向运动,则该波的传播方向是-x(选填“+x”或“-x”),经过△t=0.05s时间P点的加速度第一次达到最大且指向y轴负方向.