题目内容
15.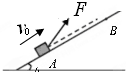 一质量m=1kg的小物块,以v0=2m/s的初速度在与斜面成370夹角大小为10N拉力F作用下,从无限长斜面底端A点向上运动,在距离A点6cn的B点撤去拉力.已知斜面倾角θ=370,物块与斜面之间的动摩擦因数为0.5,重力加速度g取10m/s2,试求物块在斜面上运动的总时间?
一质量m=1kg的小物块,以v0=2m/s的初速度在与斜面成370夹角大小为10N拉力F作用下,从无限长斜面底端A点向上运动,在距离A点6cn的B点撤去拉力.已知斜面倾角θ=370,物块与斜面之间的动摩擦因数为0.5,重力加速度g取10m/s2,试求物块在斜面上运动的总时间?
分析 物体从A到B匀加速直线运动,根据位移时间公式可求加速时间;撤去F后,物体做匀减速直线运动,根据牛顿第二定律可得减速运动的加速度,根据速度时间公式可求减速时间;最后反向匀加速直线运动,利用位移时间公式求加速下滑时间,从而求解运动的总时间.
解答 解:(1)设力F作用在物体时物体加速度的大小为a,
垂直斜面方向有平衡得:Fsin37°+FN=mgcos37° ①
由牛顿第二定律得:${a}_{1}=\frac{Fcos37°-mgsin37°-μ{F}_{N}}{m}$ ②
由位移时间公式得:${x}_{1}={v}_{0}{t}_{1}+\frac{1}{2}{a}_{1}{{t}_{1}}^{2}$ ③
代入数据①②③联立得:t1=2s
撤去力F瞬间速度为:v1=v0+a1t1=2+1×1m/s=4m/s
撤去F后,物体做匀减速直线运动,
根据牛顿第二定律可得减速运动的加速度为:
${a}_{2}=\frac{mgsin37°+μmgcos37°}{m}=gsin37°+μgcos37°=10m/{s}^{2}$
由v=v0+at得:
减速运动时间为;${t}_{2}=\frac{v-{v}_{1}}{-{a}_{2}}=\frac{0-4}{-10}s=0.4s$
减速运动的位移为:${x}_{2}=\frac{1}{2}{a}_{2}{{t}_{2}}^{2}=\frac{1}{2}×10×{0.4}^{2}m=0.8m$
反向后物体做匀加速直线运动,由牛顿第二定律得:
${a}_{3}=\frac{mgsin3{7}^{0}-μmgcos37°}{m}=2m/{s}^{2}$
根据$x=\frac{1}{2}a{t}^{2}$得:
下滑的时间为:${t}_{3}=\sqrt{\frac{2x}{{a}_{3}}}=\sqrt{\frac{2×(6+0.8)}{2}}s=2.6s$
所以下滑在斜面运动的总时间为:t=t1+t2+t3=2+0.4+2.6s=5s
答:运动的总时间为5s.
点评 本题考查牛顿第二定律和运动学公式的综合应用,关键对物体正确的受力分析,分清物体的运动过程,正确的列方程求解即可.

 宇宙间存在一些离其他恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量相等的星球位于等边三角形的三个顶点上,任意两颗星球的距离均为R,并绕其中心O做匀速圆周运动.忽略其他星球对它们的引力作用,引力常量为G,以下对该三星系统的说法不正确的是( )
宇宙间存在一些离其他恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量相等的星球位于等边三角形的三个顶点上,任意两颗星球的距离均为R,并绕其中心O做匀速圆周运动.忽略其他星球对它们的引力作用,引力常量为G,以下对该三星系统的说法不正确的是( )| A. | 每颗星球做圆周运动的半径都等于R | |
| B. | 每颗星球做圆周运动的加速度与三颗星球的质量无关 | |
| C. | 每颗星球做圆周运动的周期为T=2πR$\sqrt{\frac{R}{3Gm}}$ | |
| D. | 每颗星球做圆周运动的线速度v=$\sqrt{\frac{Gm}{R}}$ |
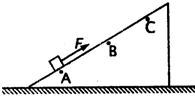 如图所示,一光滑斜面固定在水平地面上,质量m=1kg的物体在平行于斜面向上的恒力F作用下从A点由静止开始运动,到达B点时撤去拉力F,物体到达C点时速度为零.通过传感器测得每隔0.2s物体的瞬时速度如表.
如图所示,一光滑斜面固定在水平地面上,质量m=1kg的物体在平行于斜面向上的恒力F作用下从A点由静止开始运动,到达B点时撤去拉力F,物体到达C点时速度为零.通过传感器测得每隔0.2s物体的瞬时速度如表.| t/s | 0.0 | 0.2 | 0.4 | … | 2.2 | 2.4 | 2.6 | … |
| v/m•g-1 | 0.0 | 1.0 | 2.0 | … | 3.3 | 2.1 | 0.9 | … |
(2)物体沿斜面向上运动过程中的最大速度是多大?
 如图所示,在水平固定的光滑平板上,有一质量为m的质点P,与穿过中央小孔O的轻绳一端相连着.平板与小孔都是光滑的,用手拉着绳子下端,使质点做半径为a、角速度为ω0的匀速圆周运动.若绳子突然放松至某一长度b而立即被拉紧,质点就能在半径为b的圆周上做匀速圆周运动,求质点由半径a到半径b所需的时间及质点在半径为b的圆周上运动的角速度.
如图所示,在水平固定的光滑平板上,有一质量为m的质点P,与穿过中央小孔O的轻绳一端相连着.平板与小孔都是光滑的,用手拉着绳子下端,使质点做半径为a、角速度为ω0的匀速圆周运动.若绳子突然放松至某一长度b而立即被拉紧,质点就能在半径为b的圆周上做匀速圆周运动,求质点由半径a到半径b所需的时间及质点在半径为b的圆周上运动的角速度.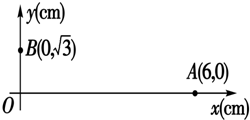 如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则
如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则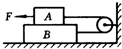 所受重力分别为G1和G2的滑块A,B,由绕过定滑轮的细绳相连后,叠放在水平桌面上,如图所示.已知A,B间的摩擦系数为μ1,B与桌面间的摩擦系数为μ2.问:
所受重力分别为G1和G2的滑块A,B,由绕过定滑轮的细绳相连后,叠放在水平桌面上,如图所示.已知A,B间的摩擦系数为μ1,B与桌面间的摩擦系数为μ2.问: 测量一个未知电阻Rx的阻值、可供使用的器材如下:
测量一个未知电阻Rx的阻值、可供使用的器材如下: