题目内容
10. 如图所示,在水平固定的光滑平板上,有一质量为m的质点P,与穿过中央小孔O的轻绳一端相连着.平板与小孔都是光滑的,用手拉着绳子下端,使质点做半径为a、角速度为ω0的匀速圆周运动.若绳子突然放松至某一长度b而立即被拉紧,质点就能在半径为b的圆周上做匀速圆周运动,求质点由半径a到半径b所需的时间及质点在半径为b的圆周上运动的角速度.
如图所示,在水平固定的光滑平板上,有一质量为m的质点P,与穿过中央小孔O的轻绳一端相连着.平板与小孔都是光滑的,用手拉着绳子下端,使质点做半径为a、角速度为ω0的匀速圆周运动.若绳子突然放松至某一长度b而立即被拉紧,质点就能在半径为b的圆周上做匀速圆周运动,求质点由半径a到半径b所需的时间及质点在半径为b的圆周上运动的角速度.
分析 (1)绳子放开后,质点沿切线方向飞出,做匀速直线运动,结合几何关系,可求运动时间;
(2)绳子放开后,质点沿切线方向飞出,做匀速直线运动,到绳子突然张紧时,将速度沿切线方向和半径方向正交分解,沿半径方向的分速度突然减为零,以切线方向的分速度绕b轨道匀速圆周运动,由牛顿第二定律和线速度与角速度的关系公式可求出角速度的大小.
解答 解:(1)绳子放开后,球沿切线方向飞出,做匀速直线运动,由几何关系,位移为:x=$\sqrt{{b}^{2}-{a}^{2}}$,
线速度为:v=ω0a;
故放开过程的时间为:t=$\frac{x}{v}$=$\frac{\sqrt{{b}^{2}-{a}^{2}}}{{ω}_{0}a}$.
(2)小球沿圆弧切线方向飞出后,到达b轨道时,绳子突然张紧,将速度沿切线方向和半径方向正交分解,沿半径方向的分速度突然减为零,以切线方向的分速度绕b轨道匀速圆周运动,由几何关系得到,由vb=vsinθ=$\frac{a}{b}$=$\frac{{a}^{2}{ω}_{0}}{b}$,则角速度ω=$\frac{{v}_{b}}{b}$=$\frac{{a}^{2}}{{b}^{2}}{ω}_{0}$;
答:质点由半径a到半径b所需的时间为$\frac{\sqrt{{b}^{2}-{a}^{2}}}{{ω}_{0}a}$.
质点在半径为b的圆周上运动的角速度为$\frac{{a}^{2}}{{b}^{2}}{ω}_{0}$.
点评 解决本题的关键知道松手后,小球沿切线方向飞出,绷紧后,沿半径方向的分速度突然减为零,以切线方向的分速度绕b轨道匀速圆周运动.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图所示,弹簧的一端固定在小车上,另一端拴在质量为1kg的物体A上,车厢底面水平.当它们都处于静止时,弹簧对物体A的水平向左拉力为0.3N,若小车以a=0.5m/s2的加速度水平向左匀加速运动时,下列说法正确的是( )
如图所示,弹簧的一端固定在小车上,另一端拴在质量为1kg的物体A上,车厢底面水平.当它们都处于静止时,弹簧对物体A的水平向左拉力为0.3N,若小车以a=0.5m/s2的加速度水平向左匀加速运动时,下列说法正确的是( )
 如图所示,弹簧的一端固定在小车上,另一端拴在质量为1kg的物体A上,车厢底面水平.当它们都处于静止时,弹簧对物体A的水平向左拉力为0.3N,若小车以a=0.5m/s2的加速度水平向左匀加速运动时,下列说法正确的是( )
如图所示,弹簧的一端固定在小车上,另一端拴在质量为1kg的物体A上,车厢底面水平.当它们都处于静止时,弹簧对物体A的水平向左拉力为0.3N,若小车以a=0.5m/s2的加速度水平向左匀加速运动时,下列说法正确的是( )| A. | 物块A相对于小车仍然静止 | B. | 物块A受到的摩擦力方向不变 | ||
| C. | 物块A受到的摩擦力大小不变 | D. | 物块A受到弹簧的拉力将增大 |
18.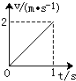 质量为0.5kg的木块在水平地面上受到水平方向外力F的作用,木块做匀加速直线运动的v-t图象如图所示,木块与地面间的动摩擦因数为0.2,g取10m/s2,则F等于( )
质量为0.5kg的木块在水平地面上受到水平方向外力F的作用,木块做匀加速直线运动的v-t图象如图所示,木块与地面间的动摩擦因数为0.2,g取10m/s2,则F等于( )
 质量为0.5kg的木块在水平地面上受到水平方向外力F的作用,木块做匀加速直线运动的v-t图象如图所示,木块与地面间的动摩擦因数为0.2,g取10m/s2,则F等于( )
质量为0.5kg的木块在水平地面上受到水平方向外力F的作用,木块做匀加速直线运动的v-t图象如图所示,木块与地面间的动摩擦因数为0.2,g取10m/s2,则F等于( )| A. | 1N | B. | 2N | C. | 3N | D. | 4N |
5. 如图所示,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到某处突然停止,此后A和B两工件的向心加速度aA和aB的大小关系是( )
如图所示,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到某处突然停止,此后A和B两工件的向心加速度aA和aB的大小关系是( )
 如图所示,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到某处突然停止,此后A和B两工件的向心加速度aA和aB的大小关系是( )
如图所示,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到某处突然停止,此后A和B两工件的向心加速度aA和aB的大小关系是( )| A. | aA=aB | B. | aA>aB | C. | aA<aB | D. | 无法比较 |
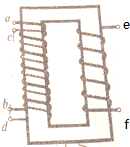 如图所示,一理想变压器的原、副线圈分别由双线圈ab和cd(匝数都为n1)及ef(匝数为n2)组成.
如图所示,一理想变压器的原、副线圈分别由双线圈ab和cd(匝数都为n1)及ef(匝数为n2)组成.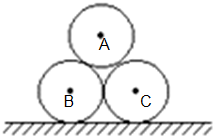 如图所示,在水平地面上放置着两个相互靠在一起的相同的圆柱形木头,在它们的上面放置同样的圆木,问圆木之间的摩擦因数至少为何值时,它们才不会滚开?(设圆木和地面无滑动现象发生 )
如图所示,在水平地面上放置着两个相互靠在一起的相同的圆柱形木头,在它们的上面放置同样的圆木,问圆木之间的摩擦因数至少为何值时,它们才不会滚开?(设圆木和地面无滑动现象发生 )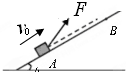 一质量m=1kg的小物块,以v0=2m/s的初速度在与斜面成370夹角大小为10N拉力F作用下,从无限长斜面底端A点向上运动,在距离A点6cn的B点撤去拉力.已知斜面倾角θ=370,物块与斜面之间的动摩擦因数为0.5,重力加速度g取10m/s2,试求物块在斜面上运动的总时间?
一质量m=1kg的小物块,以v0=2m/s的初速度在与斜面成370夹角大小为10N拉力F作用下,从无限长斜面底端A点向上运动,在距离A点6cn的B点撤去拉力.已知斜面倾角θ=370,物块与斜面之间的动摩擦因数为0.5,重力加速度g取10m/s2,试求物块在斜面上运动的总时间?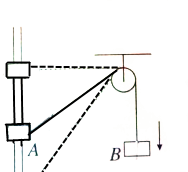 如图所示,套在竖直细杆上的环A跨过定滑轮且不可伸长的轻绳与重物B相连,由于B的质量较大,在释放B后,A将沿杆上升,当运动至定滑轮的连线处于水平位置时,其上升速度vA≠0,B未落地,这时B的速度为vB=0.
如图所示,套在竖直细杆上的环A跨过定滑轮且不可伸长的轻绳与重物B相连,由于B的质量较大,在释放B后,A将沿杆上升,当运动至定滑轮的连线处于水平位置时,其上升速度vA≠0,B未落地,这时B的速度为vB=0.