题目内容
7.“火卫一”(Phobos)呈土豆形状,围绕火星运行的周围为T,距火星中心的距离为r,它是火星两颗卫星中较大的、也是离火星较近的一颗.“火卫一”与火星间的距离也是太阳系中所有的卫星与其主星距离最短的,它也是太阳系中最小的卫星之一,已知引力常量G,将“火卫一”绕火星的轨道视为圆.求:(1)火星的质量M.
(2)已知“火卫一”与火星表面的距离为h,求火星的第一宇宙速度.
分析 根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$,化简可得火星的质量M.“火卫一”与火星表面的距离为h,则此时的轨道半径为r-h,根据万有引力提供向心力$G\frac{Mm′}{({r-h)}^{2}}=m′\frac{{v}^{2}}{r-h}$,代入火星的质量M,化简可得火星的第一宇宙速度.
解答 解:(1)“火卫一”在火星万有引力作用下做圆周运动:
$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$
解得:$M=\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$
(2)在火星表面附近,卫星在万有引力作用下做圆周运动:
$G\frac{Mm′}{({r-h)}^{2}}=m′\frac{{v}^{2}}{r-h}$
代入质量M,解得:v=$\frac{2πr}{T}\sqrt{\frac{r}{r-h}}$
答:(1)火星的质量M为$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$.
(2)火星的第一宇宙速度为$\frac{2πr}{T}\sqrt{\frac{r}{r-h}}$.
点评 本题关键是要掌握万有引力提供向心力,能够根据题意选择恰当的向心力的表达式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图所示,弹簧的一端固定在小车上,另一端拴在质量为1kg的物体A上,车厢底面水平.当它们都处于静止时,弹簧对物体A的水平向左拉力为0.3N,若小车以a=0.5m/s2的加速度水平向左匀加速运动时,下列说法正确的是( )
如图所示,弹簧的一端固定在小车上,另一端拴在质量为1kg的物体A上,车厢底面水平.当它们都处于静止时,弹簧对物体A的水平向左拉力为0.3N,若小车以a=0.5m/s2的加速度水平向左匀加速运动时,下列说法正确的是( )
 如图所示,弹簧的一端固定在小车上,另一端拴在质量为1kg的物体A上,车厢底面水平.当它们都处于静止时,弹簧对物体A的水平向左拉力为0.3N,若小车以a=0.5m/s2的加速度水平向左匀加速运动时,下列说法正确的是( )
如图所示,弹簧的一端固定在小车上,另一端拴在质量为1kg的物体A上,车厢底面水平.当它们都处于静止时,弹簧对物体A的水平向左拉力为0.3N,若小车以a=0.5m/s2的加速度水平向左匀加速运动时,下列说法正确的是( )| A. | 物块A相对于小车仍然静止 | B. | 物块A受到的摩擦力方向不变 | ||
| C. | 物块A受到的摩擦力大小不变 | D. | 物块A受到弹簧的拉力将增大 |
19. 放在水平地面上的物体受到水平拉力的作用,在0~6s内其速度与时间关系图象、所受拉力的功率与时间的关系图象如图所示,由此可求得物体的质量为(取g=10m/s2)( )
放在水平地面上的物体受到水平拉力的作用,在0~6s内其速度与时间关系图象、所受拉力的功率与时间的关系图象如图所示,由此可求得物体的质量为(取g=10m/s2)( )
 放在水平地面上的物体受到水平拉力的作用,在0~6s内其速度与时间关系图象、所受拉力的功率与时间的关系图象如图所示,由此可求得物体的质量为(取g=10m/s2)( )
放在水平地面上的物体受到水平拉力的作用,在0~6s内其速度与时间关系图象、所受拉力的功率与时间的关系图象如图所示,由此可求得物体的质量为(取g=10m/s2)( )| A. | $\frac{10}{9}$kg | B. | $\frac{9}{10}$kg | C. | $\frac{3}{5}$kg | D. | $\frac{5}{3}$kg |
17.力学中有三个基本量,下列各量中不属于基本量的是( )
| A. | 长度 | B. | 时间 | C. | 力 | D. | 质量 |
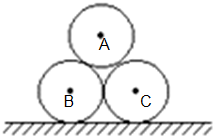 如图所示,在水平地面上放置着两个相互靠在一起的相同的圆柱形木头,在它们的上面放置同样的圆木,问圆木之间的摩擦因数至少为何值时,它们才不会滚开?(设圆木和地面无滑动现象发生 )
如图所示,在水平地面上放置着两个相互靠在一起的相同的圆柱形木头,在它们的上面放置同样的圆木,问圆木之间的摩擦因数至少为何值时,它们才不会滚开?(设圆木和地面无滑动现象发生 )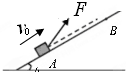 一质量m=1kg的小物块,以v0=2m/s的初速度在与斜面成370夹角大小为10N拉力F作用下,从无限长斜面底端A点向上运动,在距离A点6cn的B点撤去拉力.已知斜面倾角θ=370,物块与斜面之间的动摩擦因数为0.5,重力加速度g取10m/s2,试求物块在斜面上运动的总时间?
一质量m=1kg的小物块,以v0=2m/s的初速度在与斜面成370夹角大小为10N拉力F作用下,从无限长斜面底端A点向上运动,在距离A点6cn的B点撤去拉力.已知斜面倾角θ=370,物块与斜面之间的动摩擦因数为0.5,重力加速度g取10m/s2,试求物块在斜面上运动的总时间? 如图所示,从A点以v0=4m/s的水平速度抛出一质量为m=1kg的小物块(可视为质点),当物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,经圆弧轨道后滑上与C点等高、静止在粗糙水平面的长木板上,圆弧轨道C端切线水平.已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.5m,h=0.15m,R=0.75m,物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2,g=10m/s2,求:
如图所示,从A点以v0=4m/s的水平速度抛出一质量为m=1kg的小物块(可视为质点),当物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,经圆弧轨道后滑上与C点等高、静止在粗糙水平面的长木板上,圆弧轨道C端切线水平.已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.5m,h=0.15m,R=0.75m,物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2,g=10m/s2,求: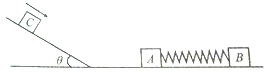 如图所示,木块A的质量为m,木块B的质量为km(k为常数),A,B由轻弹簧拴接,置于光滑水平面上,弹簧处于自然状态,一质量为m的木块C静止在木块A的左侧斜面上,木块C与斜面的动摩擦因数为μ=tanθ,斜面底端与木块A的距离足够长,现给木块C以初速度v0使之沿斜面向下运动,与A碰撞后,与A一起压缩弹簧,但与A不粘连.已知木块C返回斜面底端时的速度为$\frac{{v}_{0}}{2}$,最终静止在斜面上某处.设木块C的最大静摩擦力等于滑动摩擦力,不计木块经过斜面与平面连接处的能量损失,求:
如图所示,木块A的质量为m,木块B的质量为km(k为常数),A,B由轻弹簧拴接,置于光滑水平面上,弹簧处于自然状态,一质量为m的木块C静止在木块A的左侧斜面上,木块C与斜面的动摩擦因数为μ=tanθ,斜面底端与木块A的距离足够长,现给木块C以初速度v0使之沿斜面向下运动,与A碰撞后,与A一起压缩弹簧,但与A不粘连.已知木块C返回斜面底端时的速度为$\frac{{v}_{0}}{2}$,最终静止在斜面上某处.设木块C的最大静摩擦力等于滑动摩擦力,不计木块经过斜面与平面连接处的能量损失,求: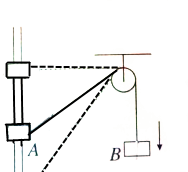 如图所示,套在竖直细杆上的环A跨过定滑轮且不可伸长的轻绳与重物B相连,由于B的质量较大,在释放B后,A将沿杆上升,当运动至定滑轮的连线处于水平位置时,其上升速度vA≠0,B未落地,这时B的速度为vB=0.
如图所示,套在竖直细杆上的环A跨过定滑轮且不可伸长的轻绳与重物B相连,由于B的质量较大,在释放B后,A将沿杆上升,当运动至定滑轮的连线处于水平位置时,其上升速度vA≠0,B未落地,这时B的速度为vB=0.