��Ŀ����
9�� ��������һЩ���������ǽ�Զ������ϵͳ��������һ������ϵͳ��ͼ��ʾ������������ȵ�����λ�ڵȱ������ε����������ϣ�������������ľ����ΪR������������O������Բ���˶�������������������ǵ��������ã���������ΪG�����¶Ը�����ϵͳ��˵������ȷ���ǣ�������
��������һЩ���������ǽ�Զ������ϵͳ��������һ������ϵͳ��ͼ��ʾ������������ȵ�����λ�ڵȱ������ε����������ϣ�������������ľ����ΪR������������O������Բ���˶�������������������ǵ��������ã���������ΪG�����¶Ը�����ϵͳ��˵������ȷ���ǣ�������| A�� | ÿ��������Բ���˶��İ뾶������R | |
| B�� | ÿ��������Բ���˶��ļ��ٶ������������������ | |
| C�� | ÿ��������Բ���˶�������ΪT=2��R$\sqrt{\frac{R}{3Gm}}$ | |
| D�� | ÿ��������Բ���˶������ٶ�v=$\sqrt{\frac{Gm}{R}}$ |
���� ��д��������������֮���������������ÿһ�������ܵ��ĺ������ú����ṩ���ǵ���������
Ȼ����R��������ǵĹ���뾶�����д�������ں����ٶȱ�����������Ĺ�ʽ���������ɵij������
��� �⣺A���ɼ��ι�ϵ֪��ÿ��������Բ���˶��İ뾶��r=$\frac{\sqrt{3}}{3}$R����A����
B��������������֮�����������F=$\frac{Gmm}{{R}^{2}}$��
һ�������ܵ��ĺ�����F1=$\sqrt{3}$F��
�����ṩ���ǵ���������$\sqrt{3}$$\frac{Gmm}{{R}^{2}}$=ma��
��ã�a=$\frac{\sqrt{3}Gm}{{R}^{2}}$�����������������m�����ȣ���B����
C�������ṩ���ǵ���������$\frac{\sqrt{3}Gmm}{{R}^{2}}$=m$\frac{4{��}^{2}}{{T}^{2}}r$����T=T=2��R$\sqrt{\frac{R}{3Gm}}$����C��ȷ��
D�������ṩ���ǵ���������$\sqrt{3}$$\frac{Gmm}{{R}^{2}}$=m$\frac{{v}^{2}}{r}$����ã�v=$\sqrt{\frac{Gm}{R}}$����D��ȷ��
����ѡ����ģ���ѡ��AB��
���� �����������Ҫ����ģ�����ṩ���龰��Ȼ���ܹ��г������ṩ�������Ĺ�ʽ��������ȷ�����Ŀ��

 ��ͼ�ף�Բ����ȦP��ֹ��ˮƽ�����ϣ������Ϸ�����һ��ͬ����ȦQ��P��Q���ᣬQ��ͨ�б仯������������ʱ��仯�Ĺ�����ͼ����ʾ��P��������ΪG��������P��֧����ΪN��������
��ͼ�ף�Բ����ȦP��ֹ��ˮƽ�����ϣ������Ϸ�����һ��ͬ����ȦQ��P��Q���ᣬQ��ͨ�б仯������������ʱ��仯�Ĺ�����ͼ����ʾ��P��������ΪG��������P��֧����ΪN��������| A�� | t1ʱ�� N��G | B�� | t2ʱ�� N��G | C�� | t3ʱ�� N��G | D�� | t4ʱ�� N=G |
 ��ͼ��ʾ�����ɵ�һ�˹̶���С���ϣ���һ��˩������Ϊ1kg������A�ϣ��������ˮƽ�������Ƕ����ھ�ֹʱ�����ɶ�����A��ˮƽ��������Ϊ0.3N����С����a=0.5m/s2�ļ��ٶ�ˮƽ�����ȼ����˶�ʱ������˵����ȷ���ǣ�������
��ͼ��ʾ�����ɵ�һ�˹̶���С���ϣ���һ��˩������Ϊ1kg������A�ϣ��������ˮƽ�������Ƕ����ھ�ֹʱ�����ɶ�����A��ˮƽ��������Ϊ0.3N����С����a=0.5m/s2�ļ��ٶ�ˮƽ�����ȼ����˶�ʱ������˵����ȷ���ǣ�������| A�� | ���A�����С����Ȼ��ֹ | B�� | ���A�ܵ���Ħ�������� | ||
| C�� | ���A�ܵ���Ħ������С���� | D�� | ���A�ܵ����ɵ����������� |

 �������ͬ�IJ���ƿA��B�ֱ�װ���¶�Ϊ60���O�����ˮ����ˮ����ͼ��ʾ��
�������ͬ�IJ���ƿA��B�ֱ�װ���¶�Ϊ60���O�����ˮ����ˮ����ͼ��ʾ�� ��ͼ��ʾ����һ�̶���ϸ������һ������Ϊm=30g�Ĺ⻬С��A���¶��ó�ΪL=1m��ϸ����һ����ΪM=50g��B����B������һ����Ϊm0=10g���ӵ����ٶ�v0=18m/s���ľ��B������B�У���B�Ժ����������߶�hΪ���٣�g=10m/s2��
��ͼ��ʾ����һ�̶���ϸ������һ������Ϊm=30g�Ĺ⻬С��A���¶��ó�ΪL=1m��ϸ����һ����ΪM=50g��B����B������һ����Ϊm0=10g���ӵ����ٶ�v0=18m/s���ľ��B������B�У���B�Ժ����������߶�hΪ���٣�g=10m/s2��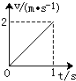 ����Ϊ0.5kg��ľ����ˮƽ�������ܵ�ˮƽ��������F�����ã�ľ�����ȼ���ֱ���˶���v-tͼ����ͼ��ʾ��ľ��������Ķ�Ħ������Ϊ0.2��gȡ10m/s2����F���ڣ�������
����Ϊ0.5kg��ľ����ˮƽ�������ܵ�ˮƽ��������F�����ã�ľ�����ȼ���ֱ���˶���v-tͼ����ͼ��ʾ��ľ��������Ķ�Ħ������Ϊ0.2��gȡ10m/s2����F���ڣ�������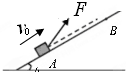 һ����m=1kg��С��飬��v0=2m/s�ij��ٶ�����б���370�нǴ�СΪ10N����F�����£�������б���A�������˶����ھ���A��6cn��B�㳷ȥ��������֪б����Ǧ�=370�������б��֮��Ķ�Ħ������Ϊ0.5���������ٶ�gȡ10m/s2�����������б�����˶�����ʱ�䣿
һ����m=1kg��С��飬��v0=2m/s�ij��ٶ�����б���370�нǴ�СΪ10N����F�����£�������б���A�������˶����ھ���A��6cn��B�㳷ȥ��������֪б����Ǧ�=370�������б��֮��Ķ�Ħ������Ϊ0.5���������ٶ�gȡ10m/s2�����������б�����˶�����ʱ�䣿