题目内容
3.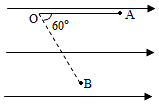 长为L细线,上端固定,下端栓一质量为m、带电量为q的球,处于如图所示的水平向右的匀强电场中,开始时,将细线与小球拉成水平,然后释放,小球由静止开始向下摆动,当细杆转动60°角时,小球到达B点,且速度恰好为零,求:
长为L细线,上端固定,下端栓一质量为m、带电量为q的球,处于如图所示的水平向右的匀强电场中,开始时,将细线与小球拉成水平,然后释放,小球由静止开始向下摆动,当细杆转动60°角时,小球到达B点,且速度恰好为零,求:(1)AB点的电势差UAB;
(2)匀强电场的电场强度E大小;
(3)小球到达B点时,细线对小球的拉力F大小.
分析 (1)小球从A到B的过程中,重力做正功mgLsin60°,电场力做功为qUAB,动能的变化量为零,根据动能定理求解电势差UAB;
(2)根据电场强度与电势差的关系U=Ed求解场强.式中d是AB沿电场线方向的距离,d=L-Lcos60°.
(3)小球在AB间摆动时具有对称性,B处绳拉力与A处绳拉力相等,研究A处绳子的拉力得到B处绳子的拉力.在A处小球水平方向平衡,由平衡条件求解拉力.
解答 解:
(1)小球由A到B过程中,由动能定理得:
mgLsin60°+qUAB=0
所以UAB=-$\frac{\sqrt{3}mgL}{2q}$;
(2)BA间电势差为UBA=-UAB=$\frac{\sqrt{3}mgL}{2q}$
则场强E=$\frac{{U}_{BA}}{L-Lcos60°}$=$\frac{\sqrt{3}mg}{q}$;
(3)小球在AB间摆动,由对称性得知,B处绳拉力与A处绳拉力相等,而在A处,由水平方向平衡有:
FTA=Eq=$\sqrt{3}$mg,
所以FTB=FTA=$\sqrt{3}$mg.
答:
(1)AB两点的电势差UAB为-$\frac{\sqrt{3}mgL}{2q}$;
(2)匀强电场的场强大小是$\frac{\sqrt{3}mg}{q}$;
(3)小球到达B点时,细线对小球的拉力大小是$\sqrt{3}$mg.
点评 本题考查带电粒子在电场和重力场中的运动,要注意明确电势差与电场强度之间的关系,明确动能定理的应用,特别是第(3)问要注意利用对称性进行分析,当然也可以直接研究B处受力得出正确答案,方法为:小球在B处,沿绳方向合力为零,有:FTB=Eqcos60°+mgcos30°=$\sqrt{3}$mg.

练习册系列答案
相关题目
13. 如图所示,垂直纸面的匀强磁场分布在正方形虚线区域内,电阻均匀的正方形导线框abcd位于虚线区域的中央,两正方形共面且四边相互平行.现将导线框先后朝图示两个方向以速度v、3v匀速拉出磁场,拉出时保持线框不离开纸面且速度垂直线框.比较两次移出磁场的过程中,以下说法正确的是( )
如图所示,垂直纸面的匀强磁场分布在正方形虚线区域内,电阻均匀的正方形导线框abcd位于虚线区域的中央,两正方形共面且四边相互平行.现将导线框先后朝图示两个方向以速度v、3v匀速拉出磁场,拉出时保持线框不离开纸面且速度垂直线框.比较两次移出磁场的过程中,以下说法正确的是( )
 如图所示,垂直纸面的匀强磁场分布在正方形虚线区域内,电阻均匀的正方形导线框abcd位于虚线区域的中央,两正方形共面且四边相互平行.现将导线框先后朝图示两个方向以速度v、3v匀速拉出磁场,拉出时保持线框不离开纸面且速度垂直线框.比较两次移出磁场的过程中,以下说法正确的是( )
如图所示,垂直纸面的匀强磁场分布在正方形虚线区域内,电阻均匀的正方形导线框abcd位于虚线区域的中央,两正方形共面且四边相互平行.现将导线框先后朝图示两个方向以速度v、3v匀速拉出磁场,拉出时保持线框不离开纸面且速度垂直线框.比较两次移出磁场的过程中,以下说法正确的是( )| A. | 导体框cd边两端电势差的大小相同 | B. | 导体框中产生的焦耳热相同 | ||
| C. | 通过导体框某一截面的电荷量不同 | D. | 导体框cd边中的感应电流方向不同 |
13. 固定的粗糙绝缘斜面上,有平行于斜面的匀强电场.一个带电体从斜面的底端,以一定的初速度沿斜面向上滑动后,又沿斜面加速下滑到底端.将带电体上滑过程与下滑过程比较( )
固定的粗糙绝缘斜面上,有平行于斜面的匀强电场.一个带电体从斜面的底端,以一定的初速度沿斜面向上滑动后,又沿斜面加速下滑到底端.将带电体上滑过程与下滑过程比较( )
 固定的粗糙绝缘斜面上,有平行于斜面的匀强电场.一个带电体从斜面的底端,以一定的初速度沿斜面向上滑动后,又沿斜面加速下滑到底端.将带电体上滑过程与下滑过程比较( )
固定的粗糙绝缘斜面上,有平行于斜面的匀强电场.一个带电体从斜面的底端,以一定的初速度沿斜面向上滑动后,又沿斜面加速下滑到底端.将带电体上滑过程与下滑过程比较( )| A. | 加速度大小相等 | B. | 滑行的时间相等 | ||
| C. | 速度改变量大小相等 | D. | 克服摩擦力做功相等 |



 半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电荷的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是重力的$\frac{3}{4}$倍.将珠子从环上的最低点A静止释放(重力加速度为g),则:
半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电荷的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是重力的$\frac{3}{4}$倍.将珠子从环上的最低点A静止释放(重力加速度为g),则: 在一个匀强电场中有A、B、C三点,AB长 为5cm,AC为3cm,BC为4cm,如图所示,电场强度方向平行于纸面,电子在电场力作用下由C运动到A,动能减少60eV,质子在电场力作用下由C运动至B,动能增加60eV,求该匀强电场的大小和方向.
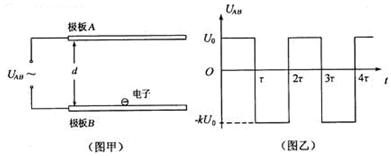
在一个匀强电场中有A、B、C三点,AB长 为5cm,AC为3cm,BC为4cm,如图所示,电场强度方向平行于纸面,电子在电场力作用下由C运动到A,动能减少60eV,质子在电场力作用下由C运动至B,动能增加60eV,求该匀强电场的大小和方向. 如图所示,质量m=5.0×10-8千克的带电粒子,以初速v0=2m/s的速度从水平放置的平行金属板A、B的中点水平飞入电场,已知金属板长0.1m,板间距离d=2×10-2m,当板间电压UAB=1000V时,带电粒子恰好沿直线穿过电场;若两极板间的电势差可调,要使粒子能从两板间飞出,板间电压UAB的变化范围是多少?(取g=10m/s2)
如图所示,质量m=5.0×10-8千克的带电粒子,以初速v0=2m/s的速度从水平放置的平行金属板A、B的中点水平飞入电场,已知金属板长0.1m,板间距离d=2×10-2m,当板间电压UAB=1000V时,带电粒子恰好沿直线穿过电场;若两极板间的电势差可调,要使粒子能从两板间飞出,板间电压UAB的变化范围是多少?(取g=10m/s2)