题目内容
13. 如图所示直角坐标xOy平面,在0≤x≤a区域Ⅰ内有沿x轴正向的匀强电场,电场强度大小为E;在x>a的区域Ⅱ中有垂直于xOy平面的匀强磁场(图中未画出),一质量为m、电量为q的正粒子,从坐标原点由静止开始自由释放,不计粒子重力,能过坐标为(a,b)的P点,则下列说法正确的是( )
如图所示直角坐标xOy平面,在0≤x≤a区域Ⅰ内有沿x轴正向的匀强电场,电场强度大小为E;在x>a的区域Ⅱ中有垂直于xOy平面的匀强磁场(图中未画出),一质量为m、电量为q的正粒子,从坐标原点由静止开始自由释放,不计粒子重力,能过坐标为(a,b)的P点,则下列说法正确的是( )| A. | 磁场方向垂直于xOy平面向里 | |
| B. | 粒子通过P点时动能为qEa | |
| C. | 磁感应强度B的大小可能为$\sqrt{\frac{2mEa}{q{b}^{2}}}$ | |
| D. | 磁感应强度B的大小可能为6$\sqrt{\frac{2mEa}{q{b}^{2}}}$ |
分析 根据左手定则判断磁感应强度的方向;根据动能定理求解粒子通过P点时的动能;粒子可能经过多个半周以后通过P点,分析粒子运动半径大小.推导出磁感应强度的计算公式进行分析.
解答  解:根据题意可得,粒子能够通过(a,b)的P点,轨迹可能的情况如图所示,
解:根据题意可得,粒子能够通过(a,b)的P点,轨迹可能的情况如图所示,
A、根据左手定则可得,磁场方向垂直于xOy平面向里,A正确;
B、洛伦兹力不做功,整个过程中只有电场力做功,根据动能定理可得,粒子通过P点时动能为Ek=qEa,B正确;
CD、粒子在磁场中运动的速度大小为v,则Ek=qEa=$\frac{1}{2}m{v}^{2}$,解得:v=$\sqrt{\frac{2qEa}{m}}$;
粒子在磁场中运动的半径为:r=$\frac{b}{2n}$,其中n=1、2、3…,
根据r=$\frac{mv}{qB}$可得:B=2n$\sqrt{\frac{2mEa}{q{b}^{2}}}$,磁感应强度不可能为$\sqrt{\frac{2mEa}{q{b}^{2}}}$;
当n=3时,B=6$\sqrt{\frac{2mEa}{q{b}^{2}}}$,所以C错误,D正确;
故选:ABD.
点评 对于带电粒子在磁场中的运动情况分析,一般是确定圆心位置,根据几何关系求半径,结合洛伦兹力提供向心力求解未知量;根据周期公式结合轨迹对应的圆心角求时间.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
18. 如图所示,质量分别为m1和m2的两个物体,m1<m2,在大小相等的两个力F1和F2的作用下沿粗糙水平面方向由静止移动相同的距离,若F1、F2做的功为W1、W2,末动能为EK1、EK2,两个物体的摩擦因数均相同,则( )
如图所示,质量分别为m1和m2的两个物体,m1<m2,在大小相等的两个力F1和F2的作用下沿粗糙水平面方向由静止移动相同的距离,若F1、F2做的功为W1、W2,末动能为EK1、EK2,两个物体的摩擦因数均相同,则( )
 如图所示,质量分别为m1和m2的两个物体,m1<m2,在大小相等的两个力F1和F2的作用下沿粗糙水平面方向由静止移动相同的距离,若F1、F2做的功为W1、W2,末动能为EK1、EK2,两个物体的摩擦因数均相同,则( )
如图所示,质量分别为m1和m2的两个物体,m1<m2,在大小相等的两个力F1和F2的作用下沿粗糙水平面方向由静止移动相同的距离,若F1、F2做的功为W1、W2,末动能为EK1、EK2,两个物体的摩擦因数均相同,则( )| A. | W1=W2、EK1=EK2 | B. | W1<W2、EK1<EK2 | ||
| C. | W1=W2、EK1>EK2 | D. | W1=W2,但动能条件不足,无法确定 |
5. 如图所示,以o为圆心的圆周上有六个等分点a、b、c、d、e、f等量正、负点电荷分别放置在a、d两处时,在它们共同形成的电场中,圆心o处产生的电场强度大小为E,下列叙述正确的是( )
如图所示,以o为圆心的圆周上有六个等分点a、b、c、d、e、f等量正、负点电荷分别放置在a、d两处时,在它们共同形成的电场中,圆心o处产生的电场强度大小为E,下列叙述正确的是( )
 如图所示,以o为圆心的圆周上有六个等分点a、b、c、d、e、f等量正、负点电荷分别放置在a、d两处时,在它们共同形成的电场中,圆心o处产生的电场强度大小为E,下列叙述正确的是( )
如图所示,以o为圆心的圆周上有六个等分点a、b、c、d、e、f等量正、负点电荷分别放置在a、d两处时,在它们共同形成的电场中,圆心o处产生的电场强度大小为E,下列叙述正确的是( )| A. | 在两个点电荷形成的电场中,e、f处场强相同 | |
| B. | 在两电荷的连线上o处场强大小最大 | |
| C. | 若仅将a处点电荷移至移至e处,o处的电场强度大小减半,方向沿oc | |
| D. | ad垂直平分线上各点的场强大小不等、方向也不相同 |
2. 10月17日神舟十一号飞船成功发射,将与天宫二号空间站进行对接,对接成功后,二者组成的整体在距地面的高度为$\frac{1}{16}$R(R为地球半径)的地方绕地球做周期为T的圆周运动,则( )
10月17日神舟十一号飞船成功发射,将与天宫二号空间站进行对接,对接成功后,二者组成的整体在距地面的高度为$\frac{1}{16}$R(R为地球半径)的地方绕地球做周期为T的圆周运动,则( )
 10月17日神舟十一号飞船成功发射,将与天宫二号空间站进行对接,对接成功后,二者组成的整体在距地面的高度为$\frac{1}{16}$R(R为地球半径)的地方绕地球做周期为T的圆周运动,则( )
10月17日神舟十一号飞船成功发射,将与天宫二号空间站进行对接,对接成功后,二者组成的整体在距地面的高度为$\frac{1}{16}$R(R为地球半径)的地方绕地球做周期为T的圆周运动,则( )| A. | 神舟十一号飞船在椭圆轨道上运动的周期可能等于80分钟 | |
| B. | 成功对接后,宇航员不动时宇航员处于平衡状态 | |
| C. | 成功对接后,空间站所处位置的重力加速度为0 | |
| D. | 可求得地球质量为($\frac{17}{16}$)3$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$ |
3.导体A带5q的正电荷,另一完全相同的导体B带-q的负电荷,将两导体接触一会后再分开,则B导体带的电荷量为( )
| A. | -q | B. | q | C. | 2q | D. | -2q |
 风洞实验室中可产生方向、大小都可以调节控制的各种风力,如图所示为某风洞里模拟做实验的示意图.一质量为m=1.0kg的小球套在一根固定的足够长直杆上,直杆与水平面夹角为30°.现小球在F=16N的竖直向上的风力作用下,从A点由静止出发沿直杆向上运动,已知杆的摩擦忽略不计,重力加速度g取10m/s,试求:
风洞实验室中可产生方向、大小都可以调节控制的各种风力,如图所示为某风洞里模拟做实验的示意图.一质量为m=1.0kg的小球套在一根固定的足够长直杆上,直杆与水平面夹角为30°.现小球在F=16N的竖直向上的风力作用下,从A点由静止出发沿直杆向上运动,已知杆的摩擦忽略不计,重力加速度g取10m/s,试求: 如图甲,倾角θ=30°的斜面固定在水平面上.t=0时,一物块从斜面顶端沿斜面下滑,t=1s时到达底端.物块在斜面上运动的v-t图象如图乙.取g=10m/s2.求:
如图甲,倾角θ=30°的斜面固定在水平面上.t=0时,一物块从斜面顶端沿斜面下滑,t=1s时到达底端.物块在斜面上运动的v-t图象如图乙.取g=10m/s2.求: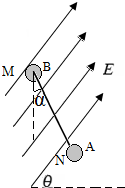 如图所示,整个装置处于真空中.一根长L=1.5m的光滑绝缘细直杆MN,与竖直方向成α=30°固定在场强大小为E=1.0×105N/C、与水平方向成θ=60°角的倾斜向上匀强电场中.杆的下端N固定一个带电小球A,电荷量Q=+4.5×10-6C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6C,质量m=1.0×10-2kg.已知真空中点电荷q周围的电势ϕ=k$\frac{q}{r}$(取无穷远处为零电势,k=9.0×109N•m2/C2).现将小球B从杆的上端M静止释放,小球B开始运动.求:(重力加速度g=10m/s2)
如图所示,整个装置处于真空中.一根长L=1.5m的光滑绝缘细直杆MN,与竖直方向成α=30°固定在场强大小为E=1.0×105N/C、与水平方向成θ=60°角的倾斜向上匀强电场中.杆的下端N固定一个带电小球A,电荷量Q=+4.5×10-6C;另一带电小球B穿在杆上可自由滑动,电荷量q=+1.0×10-6C,质量m=1.0×10-2kg.已知真空中点电荷q周围的电势ϕ=k$\frac{q}{r}$(取无穷远处为零电势,k=9.0×109N•m2/C2).现将小球B从杆的上端M静止释放,小球B开始运动.求:(重力加速度g=10m/s2)