题目内容
8. 如图,S为一离子源,MN为长荧光屏,S到MN的距离为L,这个装置处在范围足够大的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小为B.某时刻离子源S一次性沿平行纸面的各个方向均匀地射出大量的正离子,各离子质量m、电荷量q、速率v均相同,不计离子的重力及离子间的相互作用力.则( )
如图,S为一离子源,MN为长荧光屏,S到MN的距离为L,这个装置处在范围足够大的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小为B.某时刻离子源S一次性沿平行纸面的各个方向均匀地射出大量的正离子,各离子质量m、电荷量q、速率v均相同,不计离子的重力及离子间的相互作用力.则( )| A. | 当v<$\frac{qBL}{2m}$时所有离子都打不到荧光屏 | |
| B. | 当v<$\frac{qBL}{m}$时所有离子都打不到荧光屏 | |
| C. | 当v=$\frac{qBL}{m}$时,打到荧光屏MN的离子数与发射的离子总数比值为$\frac{5}{12}$ | |
| D. | 当v=$\frac{qBL}{m}$时,打到荧光屏MN的离子数与发射的离子总数比值为$\frac{1}{2}$ |
分析 根据带电粒子在磁场中做匀速圆周运动的半径公式求出离子的轨道半径,画出轨迹示意图,然后求出离子到达荧光屏上离子数与总数的比值
解答 解:A、根据半径公式$R=\frac{mv}{qB}$,当$v<\frac{qBL}{2m}$时,$R<\frac{L}{2}$,直径2R<L,离荧光屏最近的离子都打不到荧光屏上,所以当v<$\frac{qBL}{2m}$时所有离子都打不到荧光屏,故A正确;
B、根据半径公式$R=\frac{mv}{qB}$,当$v<\frac{qBL}{m}$时,R<L,当半径非常小时,即$R<\frac{L}{2}$时肯定所有离子都打不到荧光屏上;当$\frac{L}{2}≤R<L$,有离子打到荧光屏上,故B错误;
CD、当$v=\frac{qBL}{m}$时,根据半径公式$R=\frac{mv}{qB}=L$,离子运动轨迹如图所示,离子速度为${v}_{1}^{\;}$从下侧回旋,刚好和边界相切;离子速度为${v}_{2}^{\;}$时从上侧回旋,刚好和上边界相切,打到荧光屏MN的离子数与发射的离子总数比值为
,故C错误,D正确;
故选:AD
点评 本题考查了离子在磁场中的运动,离子在磁场中做匀速圆周运动,洛伦兹力提供向心力,分析清楚离子运动过程是解题的关键,应用牛顿第二定律即可解题

练习册系列答案
相关题目
20.对以a=2m/s2做匀加速直线运动的物体,下列说法正确的是( )
| A. | 2 s末速度是1s末速度的2倍 | |
| B. | 第n s末的速度比第1 s末的速度大2nm/s | |
| C. | 在任意1 s内末速度比初速度大2 m/s | |
| D. | n s时的速度是$\frac{n}{2}$s时速度的2倍 |
1. 某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )
某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )
 某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )
某质点在0~12s内运动的v-t图象如图所示.其中前4s内的图象是一段$\frac{1}{4}$圆弧,关于质点的运动,下列说法正确的是( )| A. | 质点在第一个4 s内的平均速度和在第二个4 s内的平均速度大小相等 | |
| B. | t=12 s时,质点的位移最大 | |
| C. | 质点在t=6 s时的加速度与t=10 s时的加速度大小相等,方向相反 | |
| D. | 质点在这12 s内的平均速度约为1.05 m/s |
18.(多选)一个大人(甲)跟一个小孩(乙)站在水平地面上手拉手比力气,结果大人把小孩拉过来了,对这个过程中作用于双方的力的关系,下列说法正确是( )
| A. | 大人拉小孩的力一定等于小孩拉大人的力 | |
| B. | 地对大人的摩擦力大于小孩拉大人的力 | |
| C. | 大人拉小孩的力大于地对小孩的摩擦力 | |
| D. | 地对大人的摩擦力和地对小孩的摩擦力是一对作用力 |
13.如图所示,A、B两球质量相等,A球用不能伸长的轻绳系于O点,B球用轻弹簧系于O′点,O与O′点在同一水平面上,分别将A、B球拉到与悬点等高处,使绳和轻弹簧均处于水平,弹簧处于自然状态,将两球分别由静止开始释放,当两球达到各自悬点的正下方时,两球仍处在同一水平面上;甲、乙两球质量相同,轻质悬线长度L甲>L乙,悬点等高.先将悬线拉至水平位置,再无初速地释放两球.设甲球通过最低点时的动能为EK甲,此时悬线的拉力为T甲,甲球的向心加速度为a甲,乙球通过最低点时的动能为EK乙,此时悬线的拉力为T乙,乙球的向心加速度为a乙,则下列结论中错误的是( )


| A. | EK甲>EK乙 | |
| B. | T甲=T乙 | |
| C. | a甲>a乙 | |
| D. | A、B两球到达各自悬点的正下方时,B球受到向上的拉力较小 |
18.质量为400kg的汽车沿直线以额定功率16kW从静止开始运动,经100m达到最大速度20m/s,整个过程汽车受到的阻力恒定.下列说法正确的是( )
| A. | 汽车在运动中所受到的阻力大小为400N | |
| B. | 整个过程汽车做匀加速直线运动 | |
| C. | 整个过程汽车的牵引力大小为800N | |
| D. | 整个过程汽车运动了10s |
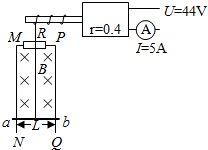 如图所示,Ⅱ字形两根足够长的平行金属导轨MN、PQ相距为L=1m,导轨平面在竖直平面,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m=2kg,导轨处于匀强磁场中,磁场的方向垂直于导轨平面,磁感应强度大小为B=1T,电阻R=10Ω,金属导轨的上端有与电机转动轴相连的绝缘轻绳,电机输入电压U=44V,工作电流恒定I=5A,线圈内阻r=0.4Ω,不计一切摩擦,不计导轨、金属棒的电阻,重力加速度为g=10m/s2,将金属棒由静止释放.
如图所示,Ⅱ字形两根足够长的平行金属导轨MN、PQ相距为L=1m,导轨平面在竖直平面,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m=2kg,导轨处于匀强磁场中,磁场的方向垂直于导轨平面,磁感应强度大小为B=1T,电阻R=10Ω,金属导轨的上端有与电机转动轴相连的绝缘轻绳,电机输入电压U=44V,工作电流恒定I=5A,线圈内阻r=0.4Ω,不计一切摩擦,不计导轨、金属棒的电阻,重力加速度为g=10m/s2,将金属棒由静止释放. 在“利用单摆测重力加速度”的实验中:
在“利用单摆测重力加速度”的实验中: