题目内容
2.火星表面特征非常接近地球,可能适合人类居住.近期,我国宇航员王跃正与俄罗斯宇航员一起进行“模拟登火星”实验活动.已知火星半径是地球半径的$\frac{1}{2}$,质量是地球质量的$\frac{1}{9}$,自转周期也基本相同.地球表面重力加速度是g,若王跃在地面上能向上跳起的最大高度是h,在忽略自转影响的条件下,下述分析正确的是( )| A. | 王跃在火星表面受的万有引力是在地球表面受万有引力的$\frac{2}{9}$倍 | |
| B. | 火星表面的重力加速度是$\frac{2g}{3}$ | |
| C. | 火星的第一宇宙速度是地球第一宇宙速度的$\frac{\sqrt{2}}{3}$倍 | |
| D. | 王跃以相同的初速度在火星上起跳时,可跳的最大高度是$\frac{3h}{2}$ |
分析 根据万有引力定律公式求出王跃在火星上受的万有引力是在地球上受万有引力的倍数.根据万有引力等于重力,得出重力加速度的关系,从而得出上升高度的关系.根据万有引力提供向心力求出第一宇宙速度的关系.
解答 解:A、根据万有引力定律的表达式F=$\frac{GMm}{{R}^{2}}$,已知火星半径是地球半径的$\frac{1}{2}$,质量是地球质量的$\frac{1}{9}$,所以王跃在火星表面受的万有引力是在地球表面受万有引力的$\frac{4}{9}$倍,故A错误.
B、由$G\frac{Mm}{{R}^{2}}=mg$,解得g=$\frac{GM}{{R}^{2}}$,已知火星半径是地球半径的$\frac{1}{2}$,质量是地球质量的$\frac{1}{9}$,火星表面的重力加速度是$\frac{4}{9}g$.故B错误.
C、根据$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$得,$v=\sqrt{\frac{GM}{R}}$,已知火星半径是地球半径的$\frac{1}{2}$,质量是地球质量的$\frac{1}{9}$,火星的第一宇宙速度是地球第一宇宙速度的$\frac{\sqrt{2}}{3}$倍,故C正确.
D、王跃以v0在地球起跳时,根据竖直上抛的运动规律得出:可跳的最大高度是 h=$\frac{{{v}_{0}}^{2}}{2g}$,由于火星表面的重力加速度是$\frac{4g}{9}$,王跃以相同的初速度在火星上起跳时,可跳的最大高度h′=$\frac{{{v}_{0}}^{2}}{2×\frac{4}{9}g}=\frac{9h}{4}$.故D错误.
故选:C.
点评 通过物理规律把进行比较的物理量表示出来,再通过已知的物理量关系求出问题是选择题中常见的方法.把星球表面的物体运动和天体运动结合起来是考试中常见的问题.

| A. | 物体受到的合外力越大,加速度越大 | |
| B. | 物体原来做匀变速直线运动,当合外力逐渐增大时,速度也一定逐渐增大 | |
| C. | 作用在物体上的合外力不为零,物体的即时速度可能为零 | |
| D. | 物体运动速度的方向总跟合外力的方向一致 |
| A. | 由E=$\frac{F}{q}$可知,某电场的场强E与q成反比,与F成正比 | |
| B. | 由 E=k$\frac{Q}{{r}^{2}}$知,某点的电场强度大小与Q成正比,与r2成反比 | |
| C. | 在真空中,点电荷Q产生的电场中,电场强度的定义式E=$\frac{F}{Q}$仍成立,式中的Q就是产生电场的点电荷 | |
| D. | 在真空中,点电荷Q产生的电场,电场强度的表达式E=$\frac{kq}{{r}^{2}}$,式中q是检验电荷的电量 |
| A. | 等于15W | B. | 大于15W | C. | 小于15W | D. | 无法确定 |
 用与竖直方向成θ角(θ<45°)的倾斜轻绳a和水平轻绳b共同固定一个小球,这时绳b的拉力为F1.现保持小球在原位置不动,使绳b在原竖直平面内逆时转过θ角后固定,绳b的拉力变为F2;再转过θ角固定,绳b的拉力为F3,则( )
用与竖直方向成θ角(θ<45°)的倾斜轻绳a和水平轻绳b共同固定一个小球,这时绳b的拉力为F1.现保持小球在原位置不动,使绳b在原竖直平面内逆时转过θ角后固定,绳b的拉力变为F2;再转过θ角固定,绳b的拉力为F3,则( )| A. | F1=F3<F2 | B. | F1=F3>F2 | C. | F1<F2<F3 | D. | Fa拉力增大 |
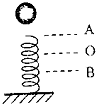 如图所示,自由下落的小球下落一段时间后,与轻质弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,即弹簧上端位置由A→O→B,且弹簧被压缩到O位置时小球所受弹力等于重力,则小球速度最大时,弹簧上端位于( )
如图所示,自由下落的小球下落一段时间后,与轻质弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,即弹簧上端位置由A→O→B,且弹簧被压缩到O位置时小球所受弹力等于重力,则小球速度最大时,弹簧上端位于( )
 矿井里的升降机,由静止开始匀加速上升,经过5s速度达到6m/s后,又以这个速度匀速上升10秒,然后匀减速上升,经过10秒恰好停在井口,则:
矿井里的升降机,由静止开始匀加速上升,经过5s速度达到6m/s后,又以这个速度匀速上升10秒,然后匀减速上升,经过10秒恰好停在井口,则: