题目内容
5. 如图所示,在倾角为θ的斜面上,轻质弹簧一端与斜面底端固定,另一端与质量为M的物体A连接,一个质量为m的物体B靠在A上,A、B与斜面的动摩擦因数均为μ.开始时用手按住物体B使弹簧处于压缩状态.现放手,使A、B一起沿斜面向上运动距离L时,A、B达到最大速度v,重力加速度为g.下列说法正确的是( )
如图所示,在倾角为θ的斜面上,轻质弹簧一端与斜面底端固定,另一端与质量为M的物体A连接,一个质量为m的物体B靠在A上,A、B与斜面的动摩擦因数均为μ.开始时用手按住物体B使弹簧处于压缩状态.现放手,使A、B一起沿斜面向上运动距离L时,A、B达到最大速度v,重力加速度为g.下列说法正确的是( )| A. | A、B达到最大速度v时,弹簧处于自然长度 | |
| B. | 若运动过程中A、B能够分离,则A、B恰好分离时,二者加速度大小均为g(sinθ+μcosθ ) | |
| C. | 从释放到A、B达到最大速度v的过程中,B受到的合力对它做的功等于$\frac{1}{2}$mv2 | |
| D. | 从释放到A、B达到最大速度v的过程中,弹簧对A所做的功等于$\frac{1}{2}$Mv2+MgLsinθ+μMgLcosθ |
分析 本题A的关键是明确A与B所受的合力为零时速度最大;题B的关键是明确A与B分离时弹簧恰好恢复原长,然后再根据牛顿第二定律即可求解;题C对物体B应用动能定理即可求解;题D对平板A列出动能定理表达式即可求解.
解答 解:A:对物体B和平板A整体分析可知,A和B达到最大速度时加速度为零,应满足kx=(m+M)gsinθ+μ(m+M)gcosθ,说明弹簧仍处于压缩状态,所以A错误;
B:根据题意可知,A和B恰好分离时,弹簧正好恢复原长,对A和B整体由牛顿第二定律得:
(m+M)gsinθ+μ(m+M)gcosθ=(m+M)a,
解得:a=gsinθ+μgcosθ=g(sinθ+cosθ),所以B正确;
C:对B从释放到A和B达到最大速度的过程由动能定理可得:${W}_{总}=\frac{1}{2}m{v}^{2}-0$,即B受到的合力对它做的功等于$\frac{1}{2}m{v}^{2}$,所以C正确;
D:对A从释放到速度达到最大的过程由动能定理可得:W弹-Mg(xm-x)sinθ-μMg(xm-x)cosθ-${F}_{N}({x}_{m}-x)=\frac{1}{2}M{v}^{2}$,
其中xm,是弹簧压缩的最大长度,x是速度最大时弹簧压缩的长度,FN是B对A的压力大小,
比较可知D错误,
故选:BC.
点评 应明确:①对物体的动态分析可知加速度为零时速度最大;②涉及到有关动能、功等问题应用动能定理求解.

练习册系列答案
相关题目
9.已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G.有关同步卫星,下列表述正确的是( )
| A. | 卫星距地面的高度为$\root{3}{\frac{GM{T}^{2}}{4{π}^{2}}}$ | |
| B. | 卫星的运行速度等于第一宇宙速度 | |
| C. | 卫星运行时受到的向心力大小为G$\frac{Mm}{{R}^{2}}$ | |
| D. | 卫星运行的向心加速度小于地球表面的重力加速度 |
10. 如图甲所示,在光滑水平面上的两小球A、B发生正碰,小球A的质量为m1=0.1kg.图乙为它们碰撞前后两个小球的s-t图象.由此可以判断( )
如图甲所示,在光滑水平面上的两小球A、B发生正碰,小球A的质量为m1=0.1kg.图乙为它们碰撞前后两个小球的s-t图象.由此可以判断( )
 如图甲所示,在光滑水平面上的两小球A、B发生正碰,小球A的质量为m1=0.1kg.图乙为它们碰撞前后两个小球的s-t图象.由此可以判断( )
如图甲所示,在光滑水平面上的两小球A、B发生正碰,小球A的质量为m1=0.1kg.图乙为它们碰撞前后两个小球的s-t图象.由此可以判断( )| A. | 碰前小球B静止,小球A向右运动 | B. | 碰后小球A和B都向右运动 | ||
| C. | 小球B的质量为m2=0.2kg | D. | 小球B的质量为m2=0.3kg |
17.如图甲所示为一列简谐横波在t=1s时的波形图,图乙是这列波中P点的振动图象,那么该波的传播方向和传播速度是( )


| A. | 沿x轴正方向传播,v=0.25 m/s | B. | 沿x轴负方向传播,v=0.50 m/s | ||
| C. | 沿x轴负方向传播,v=0.25 m/s | D. | 沿x轴正方向传播,v=0.50 m/s |
14. 如图所示,在匀强电场中有六个点A、B、C、D、E、F,正好构成一正六边形,六边形边长为0.1m,所在平面与电场方向平行.点B、C、E的电势分别为-20V、20V和60V.一带电粒子从A点以某一速度沿AB方向射出后,经过1×10-6s到达D点.不计重力.则下列判断正确的是( )
如图所示,在匀强电场中有六个点A、B、C、D、E、F,正好构成一正六边形,六边形边长为0.1m,所在平面与电场方向平行.点B、C、E的电势分别为-20V、20V和60V.一带电粒子从A点以某一速度沿AB方向射出后,经过1×10-6s到达D点.不计重力.则下列判断正确的是( )
 如图所示,在匀强电场中有六个点A、B、C、D、E、F,正好构成一正六边形,六边形边长为0.1m,所在平面与电场方向平行.点B、C、E的电势分别为-20V、20V和60V.一带电粒子从A点以某一速度沿AB方向射出后,经过1×10-6s到达D点.不计重力.则下列判断正确的是( )
如图所示,在匀强电场中有六个点A、B、C、D、E、F,正好构成一正六边形,六边形边长为0.1m,所在平面与电场方向平行.点B、C、E的电势分别为-20V、20V和60V.一带电粒子从A点以某一速度沿AB方向射出后,经过1×10-6s到达D点.不计重力.则下列判断正确的是( )| A. | 粒子带正电 | |
| B. | 粒子在A点射出时的速度为5×105m/s | |
| C. | 粒子在A点的电势能大于在D点的电势能 | |
| D. | 该粒子的比荷(电荷量与质量比值)为7.5×108C/kg |
15.许多科学家对物理学的发展作出了巨大贡献,也创造出了许多物理学方法,如理想实验法、控制变量法、极限思想法、建立物理模型法、类比法和科学假说法等等.以下关于物理学史和所用物理学方法的叙述正确的是( )
| A. | 伽利略猜想自由落体的运动速度与下落时间成正比,并直接用实验进行了验证 | |
| B. | 伽利略通过“理想斜面实验”,科学地推理出“力不是维持物持物体运动的原因” | |
| C. | 在不需要考虑物体本身的形状和大小时,用质点来代替物体的方法叫假设法 | |
| D. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加之和代表物体的位移,这里采用了微元法 |
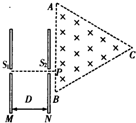 如图所示,M、N为中心开有小孔的平行板电容器的两极板,相距为D,其右侧有一边长为2a的正三角形区域,区域内有垂直纸面向里的匀强磁场,在极板M、N之间加上电压U后,M板电势高于N板电势.现有一带正电的粒子,质量为m、电荷量为q,其重力和初速度均忽略不计,粒子从极板M的中央小孔S1处射入电容器,穿过小孔S2后从距三角形A点$\sqrt{3}$a的P处垂直AB方向进入磁场,试求:
如图所示,M、N为中心开有小孔的平行板电容器的两极板,相距为D,其右侧有一边长为2a的正三角形区域,区域内有垂直纸面向里的匀强磁场,在极板M、N之间加上电压U后,M板电势高于N板电势.现有一带正电的粒子,质量为m、电荷量为q,其重力和初速度均忽略不计,粒子从极板M的中央小孔S1处射入电容器,穿过小孔S2后从距三角形A点$\sqrt{3}$a的P处垂直AB方向进入磁场,试求: 北京时间3月14日消息,2015短道速滑世锦赛于今晚在俄罗斯首都莫斯科展开了首个决赛日的争夺,在女子500米决赛中,接连有选手意外摔倒,由于短道速滑在比赛中很难超越对手,因而在比赛开始阶段每个选手都要以最大的加速度加速,在过弯道前超越对手,如果赛道的直道长度为L=30m,弯道半径为R=3m的圆弧形状,在弯道时,忽略冰面对选手的摩擦力,选手的运动视为匀速圆周运动,且地面对人的弹力沿身体方向,身体与冰面的夹角θ为30°,直线加速过程视为匀加速过程,加速度a=1m/s2,若比赛过程中选手没有减速过程,为保证比赛不出现意外情况,选手在直道上加速的最长距离为多少?(g取10m/s2)
北京时间3月14日消息,2015短道速滑世锦赛于今晚在俄罗斯首都莫斯科展开了首个决赛日的争夺,在女子500米决赛中,接连有选手意外摔倒,由于短道速滑在比赛中很难超越对手,因而在比赛开始阶段每个选手都要以最大的加速度加速,在过弯道前超越对手,如果赛道的直道长度为L=30m,弯道半径为R=3m的圆弧形状,在弯道时,忽略冰面对选手的摩擦力,选手的运动视为匀速圆周运动,且地面对人的弹力沿身体方向,身体与冰面的夹角θ为30°,直线加速过程视为匀加速过程,加速度a=1m/s2,若比赛过程中选手没有减速过程,为保证比赛不出现意外情况,选手在直道上加速的最长距离为多少?(g取10m/s2)