��Ŀ����
12��һ�����ij���ɾ�ֹ�ͷţ���ʱ��t��ʼ��ˮƽ������ײ���������־�ʱ��$\frac{1}{3}$tǡ�õ�����ߵ㣮�����˶����������ܿ��������Ĵ�С���䣬�������ײʱ�伫�̣�����ײǰ���ܲ��䣬����˵����ȷ���ǣ�������| A�� | �������������߶����½������߶ȵ�$\frac{1}{3}$ | |
| B�� | �����ܵ��Ŀ���������������������$\frac{1}{3}$ | |
| C�� | �������������е�ƽ���ٶ����½������е�ƽ���ٶȴ�С��� | |
| D�� | �������������еĻ�е����ʧ�����½������л�е����ʧ��$\frac{1}{3}$ |
���� �����������ȼ���ֱ���˶����������ȼ����˶�������λ�Ƶ���ƽ���ٶȳ���ʱ�����������������߶�֮�ȣ����ٶȹ�ʽ���������������ٶ�֮�ȣ�����ţ�ٵڶ����������������������֮�ȣ����ݹ��ܹ�ϵ�������������е����ʧ֮�ȣ�
��� �⣺AC�������������ȼ���ֱ���˶����������ȼ����˶�����������ˮƽ������ײǰ˲���ٶȴ�СΪv��
���½������е�ƽ���ٶȴ�С $\overline{{v}_{1}}$=$\frac{0+v}{2}$=$\frac{v}{2}$���������������е�ƽ���ٶ� $\overline{{v}_{2}}$=$\frac{v+0}{2}$=$\frac{v}{2}$����$\overline{{v}_{1}}$=$\overline{{v}_{2}}$��
�½������߶� h1=$\overline{{v}_{1}}$t�����������߶� h2=$\overline{{v}_{2}}$•$\frac{1}{3}$t����� h2=$\frac{1}{3}$h1����AC��ȷ��
B�����½����������ٶȴ�С�ֱ�Ϊa1��a2��
�� a1=$\frac{v}{t}$��a2=$\frac{v}{\frac{1}{3}t}$���� a2=3a1��
����ţ�ٵڶ����ɵã�
�½������У�mg-f=ma1��
����������mg+f=ma2��
������� f=$\frac{1}{2}$mg����B����
D���½������л�е����ʧ��E1=fh1�����������еĻ�е����ʧ��E2=h2f����ã���E2=$\frac{1}{3}$��E1����D��ȷ��
��ѡ��ACD
���� ����ؼ�Ҫ�������С����˶������ץס�½���ĩ�ٶȴ�С�������ij��ٶȴ�С��ȣ����ѡȡ�˶�ѧ��ʽ��ƽ���ٶȹ�ϵ��

| A�� | �����ǵĹ�ת���ٶȱȵ���С | |
| B�� | �����ǵ�����ԼΪ����������3.61�� | |
| C�� | �����ǵ�һ�����ٶ�Ϊ7.9km/s | |
| D�� | Ҫ�ڵ����Ϸ��亽����������������ٶ�ֻ��ﵽ����ĵڶ������ٶȼ��� |
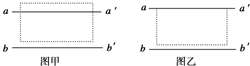 �����ò��뷨�ⶨ����ש�����ʵ�ʵ���У���ͬѧ��ֽ����ȷ��������ש����������aa���bb���С�����˲���שʹ����aa�䷽��ƽ������������ͼ����ʾ����ͬѧ�ڻ�����ʱ����С�Ľ�������aa�䡢bb����ñȲ���ש���ȴ�Щ����ͼ����ʾ��������
�����ò��뷨�ⶨ����ש�����ʵ�ʵ���У���ͬѧ��ֽ����ȷ��������ש����������aa���bb���С�����˲���שʹ����aa�䷽��ƽ������������ͼ����ʾ����ͬѧ�ڻ�����ʱ����С�Ľ�������aa�䡢bb����ñȲ���ש���ȴ�Щ����ͼ����ʾ��������| A�� | �ײ��������ƫ���Ҳ��������ƫС | |
| B�� | �ײ��������ƫС���Ҳ�������ʲ��� | |
| C�� | �ײ�������ʲ��䣬�Ҳ��������ƫС | |
| D�� | �ײ�������ʲ��䣬�Ҳ�������ʲ��� |
| A�� | ���������κ�������ܵ��������ij��������෴ | |
| B�� | ���������κ�������ܵ��������������Ĵ�С��� | |
| C�� | ������������ܵ������ij���С���������ܵ������ij��� | |
| D�� | ������׳��������׳��㣬�����仯�ķ������� |
| A�� | ����������֮����������� | B�� | ����������֮���������С | ||
| C�� | �����˶������ڲ��� | D�� | �����˶������ڼ�С |

| A�� | $\frac{{x}_{1}+{x}_{2}}{{x}_{2}}$ | B�� | $\frac{2{x}_{1}{x}_{2}}{{x}_{1}+{x}_{2}}$ | C�� | $\frac{3{x}_{1}+4{x}_{2}}{4}$ | D�� | $\frac{5{x}_{1}+{x}_{2}}{4}$ |
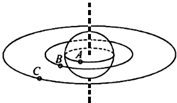 �ҹ���2015��������ŵ���ͬ������߷ֱ��ʶԵع۲����Ǹ߷��ĺţ���ͼ��ʾ��A�Ǿ�ֹ�ڳ�����������ת�����壬B��C��ͬ�ڳ��ƽ���ڵ������������ǣ�Bλ����ظ߶ȵ��ڵ���뾶��Բ�ι���ϣ�C�Ǹ߷��ĺ����ǣ��������ж���ȷ���ǣ�������
�ҹ���2015��������ŵ���ͬ������߷ֱ��ʶԵع۲����Ǹ߷��ĺţ���ͼ��ʾ��A�Ǿ�ֹ�ڳ�����������ת�����壬B��C��ͬ�ڳ��ƽ���ڵ������������ǣ�Bλ����ظ߶ȵ��ڵ���뾶��Բ�ι���ϣ�C�Ǹ߷��ĺ����ǣ��������ж���ȷ���ǣ�������| A�� | ����B�����ٶȴ�������C�����ٶ� | |
| B�� | ����A�������ת�����ڴ�������C������ | |
| C�� | ����A�������ת�ļ��ٶȴ�������C�ļ��ٶ� | |
| D�� | ����A�������ת�Ľ��ٶȴ�������B�Ľ��ٶ� |
 ��ͼ��ʾΪһ��С�����������˻�������һ���ܹ���ֱ��С��ң�ط�������Ŀǰ���õ�Խ��Խ�㷺��Ӧ�ã����˻�������Ϊm=2kg���ٶ��˶����������ܿ���������С��Ϊf=4N�������˻��ڵ����ϴӾ�ֹ��ʼ�������������ֱ������ɣ���ʱ��t=4sʱ�������ĸ߶�Ϊh=48m��gȡ10m/s2��
��ͼ��ʾΪһ��С�����������˻�������һ���ܹ���ֱ��С��ң�ط�������Ŀǰ���õ�Խ��Խ�㷺��Ӧ�ã����˻�������Ϊm=2kg���ٶ��˶����������ܿ���������С��Ϊf=4N�������˻��ڵ����ϴӾ�ֹ��ʼ�������������ֱ������ɣ���ʱ��t=4sʱ�������ĸ߶�Ϊh=48m��gȡ10m/s2��