题目内容
14. 某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )| A. | 加速时动力的大小等于mg | |
| B. | 加速与减速时的加速度大小之比为2:$\sqrt{3}$ | |
| C. | 加速与减速过程发生的位移大小之比为1:2 | |
| D. | 减速飞行时间t后速度为零 |
分析 起飞时,飞行器受推力和重力,两力的合力与水平方向成30°角斜向上,根据几何关系求出合力,由牛顿第二定律求出加速度,根据匀加速运动速度公式求解最大速度;推力方向逆时针旋转60°后,先根据牛顿第二定律求解加速度,再求出继续上升的时间.
解答 解:A、起飞时,飞行器受推力和重力,两力的合力与水平方向成30°角斜向上,设动力为F,合力为Fb,如图所示: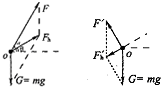
在△OFFb中,由几何关系得:F=$\sqrt{3}$mg,Fb=mg,A错误
B、由牛顿第二定律得飞行器的加速度为:a1=g,
推力方向逆时针旋转60°,合力的方向与水平方向成30°斜向下,推力F'跟合力F'h垂直,如图所示,
此时合力大小为:
F'h=mgsin30°
动力大小:
F′=$\frac{\sqrt{3}}{2}$mg
飞行器的加速度大小为:
a2=$\frac{mgsin30°}{m}$=0.5g
加速与减速时的加速度大小之比为a1:a2=2:1,B错误
C、t时刻的速率:v=a1t=gt
加速与减速过程发生的位移大小之比为$\frac{{V}^{2}}{2{a}_{1}}:\frac{{V}^{2}}{2{a}_{2}}$=1:2,故C正确
D、到最高点的时间为:t′=$\frac{V}{{a}_{2}}=\frac{gt}{0.5g}$=2t,D错误
故选:C.
点评 本题主要考查了牛顿第二定律及运动学基本公式的应用,要求同学们能正确对分析器进行受力分析并能结合几何关系求解,难度适中.

练习册系列答案
相关题目
19. 如图所示,台秤上放一光滑平板,其左边固定一挡板,一轻质弹簧将挡板和一条形磁铁连接起来,此时台秤有一定的读数.现在磁铁上方中心偏右位置固定一通电导线,当通以一定的电流后,台秤的示数增加,同时弹簧缩短(弹簧始终处于弹性限度内),则下列说法正确的是( )
如图所示,台秤上放一光滑平板,其左边固定一挡板,一轻质弹簧将挡板和一条形磁铁连接起来,此时台秤有一定的读数.现在磁铁上方中心偏右位置固定一通电导线,当通以一定的电流后,台秤的示数增加,同时弹簧缩短(弹簧始终处于弹性限度内),则下列说法正确的是( )
 如图所示,台秤上放一光滑平板,其左边固定一挡板,一轻质弹簧将挡板和一条形磁铁连接起来,此时台秤有一定的读数.现在磁铁上方中心偏右位置固定一通电导线,当通以一定的电流后,台秤的示数增加,同时弹簧缩短(弹簧始终处于弹性限度内),则下列说法正确的是( )
如图所示,台秤上放一光滑平板,其左边固定一挡板,一轻质弹簧将挡板和一条形磁铁连接起来,此时台秤有一定的读数.现在磁铁上方中心偏右位置固定一通电导线,当通以一定的电流后,台秤的示数增加,同时弹簧缩短(弹簧始终处于弹性限度内),则下列说法正确的是( )| A. | 磁铁右端为N极,左端为S极,导线中的电流方向垂直纸面向内 | |
| B. | 磁铁右端为N极,左端为S极,导线中的电流方向垂直纸面向外 | |
| C. | 磁铁右端为S极,左端为N极,导线中的电流方向垂直纸面向内 | |
| D. | 磁铁右端为S极,左端为N极,导线中的电流方向垂直纸面向外 |
1.在赤道上空,沿东西向水平放置一根通以自东向西电流的导线,则此导线( )
| A. | 受到竖直向上的安培力 | B. | 受到竖直向下的安培力 | ||
| C. | 受到由南向北的安培力 | D. | 受到由西向东的安培力 |
 跳伞员常常采用“加速自由降落”(即AFF)的方法跳伞.如果一个质量为50kg的运动员在3658m的高度从飞机上跳出,自由降落40s时,竖直向下的速度达到50m/s,然后再打开降落伞(开伞时间不计),假设这一运动是匀加速直线运动.求:
跳伞员常常采用“加速自由降落”(即AFF)的方法跳伞.如果一个质量为50kg的运动员在3658m的高度从飞机上跳出,自由降落40s时,竖直向下的速度达到50m/s,然后再打开降落伞(开伞时间不计),假设这一运动是匀加速直线运动.求: 如图,水平放置的两条平行金属导轨MN和PQ上(导轨电阻不计),静止放着两条与导轨垂直的滑杆ad和bc,导轨间距为l,两滑杆距离为d.两滑杆的质量都是m,与导轨的动摩擦因数均为μ,两滑杆电阻均为R.空间有一匀强磁场垂直轨道平面向上,磁感应强度B=B0+kt(k>0).已知重力加速度为g.求:
如图,水平放置的两条平行金属导轨MN和PQ上(导轨电阻不计),静止放着两条与导轨垂直的滑杆ad和bc,导轨间距为l,两滑杆距离为d.两滑杆的质量都是m,与导轨的动摩擦因数均为μ,两滑杆电阻均为R.空间有一匀强磁场垂直轨道平面向上,磁感应强度B=B0+kt(k>0).已知重力加速度为g.求: 如图所示,GA=100N,GB=40N,弹簧的劲度系数k=500N/m,不计绳重和摩擦,稳定后物体A对地面的压力大小为60N;弹簧的伸长量是0.08m.
如图所示,GA=100N,GB=40N,弹簧的劲度系数k=500N/m,不计绳重和摩擦,稳定后物体A对地面的压力大小为60N;弹簧的伸长量是0.08m. 用水平力F=30N拉着一个质量为2kg的物体在水平面上由静止做匀加速直线运动,某时刻将力F随时间均匀减小.整个过程物体所受的摩擦力随时间变化如图中实线所示,求:
用水平力F=30N拉着一个质量为2kg的物体在水平面上由静止做匀加速直线运动,某时刻将力F随时间均匀减小.整个过程物体所受的摩擦力随时间变化如图中实线所示,求: