题目内容
5. 如图,水平放置的两条平行金属导轨MN和PQ上(导轨电阻不计),静止放着两条与导轨垂直的滑杆ad和bc,导轨间距为l,两滑杆距离为d.两滑杆的质量都是m,与导轨的动摩擦因数均为μ,两滑杆电阻均为R.空间有一匀强磁场垂直轨道平面向上,磁感应强度B=B0+kt(k>0).已知重力加速度为g.求:
如图,水平放置的两条平行金属导轨MN和PQ上(导轨电阻不计),静止放着两条与导轨垂直的滑杆ad和bc,导轨间距为l,两滑杆距离为d.两滑杆的质量都是m,与导轨的动摩擦因数均为μ,两滑杆电阻均为R.空间有一匀强磁场垂直轨道平面向上,磁感应强度B=B0+kt(k>0).已知重力加速度为g.求:(1)t=0时刻回路中产生的感应电流大小及方向;
(2)经过多少时间,两滑杆开始滑动;
(3)从t=0至两滑杆开始滑动,整个系统产生的总热量.
分析 (1)根据法拉第电磁定律求得感应电动势的大小,再有欧姆定律求解电流的大小,根据楞次定律求解电流方向,
(2)根据二力平衡知识点结合感应电动势的大小的表达式,求解经历的时间;
(3)由焦耳定律的表达式求解产生的焦耳热;
解答 解:(1)根据法拉第电磁定律得t=0时感应电动势的大小为:
$E=\frac{△∅}{△t}=\frac{△BS}{△t}=kdl$,
由欧姆定律得,电流的大小为:
$i=\frac{E}{{R}_{总}}=\frac{kdl}{2R}$,
楞次定律的感应电流的方向:a→b→c→d→a;
(2)水平方向上,导体棒受安培力和摩擦力,由二力平衡知识得,当F安=f=μmg时,滑杆开始运动,Bil=μmg,即:$({B}_{0}+kt)\frac{kdl}{2R}l=μmg$,
解得:$t=\frac{2μmgR}{{{k^2}d{l^2}}}-\frac{B_0}{k}$;
(3)由焦耳定律得:$Q={I_感}^2•2R•t={(\frac{kdl}{2R})^2}•2R•(\frac{2μmgR}{{{k^2}d{l^2}}}-\frac{B_0}{k})=μmgd-\frac{{k{d^2}{l^2}{B_0}}}{2R}$.
答:(1)t=0时刻回路中产生的感应电流大小为$\frac{kdl}{2R}$,方向a→b→c→d→a;
(2)经过$\frac{2μmgR}{{k}^{2}d{l}^{2}}-\frac{{B}_{0}}{k}$,两滑杆开始滑动;
(3)从t=0至两滑杆开始滑动,整个系统产生的总热量为$μmgd-\frac{k{d}^{2}{l}^{2}{B}_{0}}{2R}$.
点评 本题考查了牛顿运动定律、闭合电路殴姆定律,安培力公式、感应电动势公式,在解题时要注意欧姆定律的综合题目,要熟练掌握各规律的应用.

| 额定车速 | 整车质量 | 载重 | 额定输出功率 | 电动机额定工作电压和电流 |
| 18km/h | 40kg | 80kg | 180W | 36V/6A |
(1)此电动机的电阻是多少?正常工作时,电动机的效率是多少?
(2)在水平平直道路上行驶过程中电动自行车受阻力是车重(包括载重)的k倍,试计算k的大小.
(3)仍在上述道路上行驶,若电动自行车满载时以额定功率行驶,当车速为2m/s时的加速度为多少?
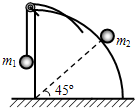 如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )
如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | 2 | D. | $\sqrt{2}$ |
 如图,在竖直平面内有一竖直向上的匀强电场,电场强度为E.一个质量为m、带电量为+q的滑块B沿斜面体表面向下匀速运动,斜面体A静止在水平地面上.已知重力加速度为g,且mg>Eq.则下列说法正确的是( )
如图,在竖直平面内有一竖直向上的匀强电场,电场强度为E.一个质量为m、带电量为+q的滑块B沿斜面体表面向下匀速运动,斜面体A静止在水平地面上.已知重力加速度为g,且mg>Eq.则下列说法正确的是( )| A. | 斜面体A受到地面的静摩擦力方向向左 | |
| B. | 匀强电场大小不变,方向改为竖直向下,则滑块B加速下滑,斜面体A受到地面的静摩擦力方向向左 | |
| C. | 匀强电场大小不变,方向改为水平向左,则滑块B加速下滑,与电场方向竖直向上时相比,斜面体A受到地面的支持力减小 | |
| D. | 匀强电场大小不变,方向改为水平向右,则滑块B减速下滑,与电场方向竖直向上时相比,斜面体A受到地面的支持力增大 |
 如图所示,在两等量异种点电荷的电场中,MN 为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a与c关于MN对称,b点位于MN上,d点位于两电荷的连线上且靠近正电荷一侧.以下判断正确的是( )
如图所示,在两等量异种点电荷的电场中,MN 为两电荷连线的中垂线,a、b、c三点所在直线平行于两电荷的连线,且a与c关于MN对称,b点位于MN上,d点位于两电荷的连线上且靠近正电荷一侧.以下判断正确的是( )| A. | 试探电荷+q在a点的电势能小于在c点的电势能 | |
| B. | a、b两点间的电势差等于b、c两点间的电势差 | |
| C. | b点场强比d点场强大 | |
| D. | b点电势比d点电势高 |
 一物体在竖直方向的升降机中,由静止开始竖直向上作直线运动,运动过程中小球的机械能E与其上升高度h关系的图象如图所示,其中0~h1过程的图线为曲线,h1~h2过程中的图线为直线.根据该图象,下列说法正确的是( )
一物体在竖直方向的升降机中,由静止开始竖直向上作直线运动,运动过程中小球的机械能E与其上升高度h关系的图象如图所示,其中0~h1过程的图线为曲线,h1~h2过程中的图线为直线.根据该图象,下列说法正确的是( )| A. | 0~h1过程中,小球的动能一定在增加 | |
| B. | 0~h1过程中,升降机对小球的支持力一定做正功 | |
| C. | h1~h2过程中,小球的动能可能在不变 | |
| D. | h1~h2过程中,小球重力势能可能不变 |
 某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )| A. | 加速时动力的大小等于mg | |
| B. | 加速与减速时的加速度大小之比为2:$\sqrt{3}$ | |
| C. | 加速与减速过程发生的位移大小之比为1:2 | |
| D. | 减速飞行时间t后速度为零 |
 如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则小船经过B点时的速度大小为$\sqrt{{v^2}+2(Pt-fd)/m}$,小船经过B点时的加速度大小为$\frac{P}{{\sqrt{{m^2}{v^2}+2m(Pt-fd)}}}-\frac{f}{m}$.
如图,用跨过光滑定滑轮的缆绳将海面上一艘小船直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船所受到水的阻力大小恒为f,经过A点时的速度大小为v,小船从A点沿直线运动到B点经历时间为t,此时缆绳与水平面夹角为θ,A、B两点间水平距离为d,缆绳质量忽略不计.则小船经过B点时的速度大小为$\sqrt{{v^2}+2(Pt-fd)/m}$,小船经过B点时的加速度大小为$\frac{P}{{\sqrt{{m^2}{v^2}+2m(Pt-fd)}}}-\frac{f}{m}$.