题目内容
6. 用水平力F=30N拉着一个质量为2kg的物体在水平面上由静止做匀加速直线运动,某时刻将力F随时间均匀减小.整个过程物体所受的摩擦力随时间变化如图中实线所示,求:
用水平力F=30N拉着一个质量为2kg的物体在水平面上由静止做匀加速直线运动,某时刻将力F随时间均匀减小.整个过程物体所受的摩擦力随时间变化如图中实线所示,求:(1)物体做匀加速直线运动的加速度;
(2)整个过程物体运动的时间;
(3)物体做匀加速直线运动发生的位移.
分析 用水平力F拉着一物体在水平地面上做匀速运动,从某时刻起力F随时间均匀减小,物体先做减速运动,所受摩擦力为滑动摩擦力,当物体速度为零后,物体受静摩擦力.
解答 解:(1)由牛顿第二定律知:
$a=\frac{F-{F}_{f}}{m}=\frac{30-20}{2}$=5m/s2
(2)由图象知物体静止时用时30s,所以运动时间30s
(3)加速时间为10s,所以有:
$x=\frac{1}{2}a{t}^{2}=0.5×5×1{0}^{2}$=250m
答:(1)物体做匀加速直线运动的加速度5m/s2;
(2)整个过程物体运动的时间30s;
(3)物体做匀加速直线运动发生的位移250m.
点评 解决本题的关键知道物体做匀速直线运动,拉力减小后,先做减速运动,最终静止.摩擦力由滑动摩擦力变为静摩擦力.

练习册系列答案
相关题目
16.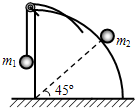 如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )
如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )
 如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )
如图所示,光滑水平面上,有一$\frac{1}{4}$的球体,球体的左侧面也光滑.质量分别为m1、m2的物体(均可看作质点),通过柔软光滑的轻绳连接,与球体一起以共同的速度v0向左匀速运动,此时m2与球心O的连线与水平线成45°.m2与球面间的动摩擦因数为0.5,设m2与球面间的最大静摩擦力等于滑动摩擦力,则$\frac{m_2}{m_1}$的最小值是( )| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | 2 | D. | $\sqrt{2}$ |
17. 一物体在竖直方向的升降机中,由静止开始竖直向上作直线运动,运动过程中小球的机械能E与其上升高度h关系的图象如图所示,其中0~h1过程的图线为曲线,h1~h2过程中的图线为直线.根据该图象,下列说法正确的是( )
一物体在竖直方向的升降机中,由静止开始竖直向上作直线运动,运动过程中小球的机械能E与其上升高度h关系的图象如图所示,其中0~h1过程的图线为曲线,h1~h2过程中的图线为直线.根据该图象,下列说法正确的是( )
 一物体在竖直方向的升降机中,由静止开始竖直向上作直线运动,运动过程中小球的机械能E与其上升高度h关系的图象如图所示,其中0~h1过程的图线为曲线,h1~h2过程中的图线为直线.根据该图象,下列说法正确的是( )
一物体在竖直方向的升降机中,由静止开始竖直向上作直线运动,运动过程中小球的机械能E与其上升高度h关系的图象如图所示,其中0~h1过程的图线为曲线,h1~h2过程中的图线为直线.根据该图象,下列说法正确的是( )| A. | 0~h1过程中,小球的动能一定在增加 | |
| B. | 0~h1过程中,升降机对小球的支持力一定做正功 | |
| C. | h1~h2过程中,小球的动能可能在不变 | |
| D. | h1~h2过程中,小球重力势能可能不变 |
14. 某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
 某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )
某科研单位设计了一空间飞行器,飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰恰与水平方向成θ=30°角的直线斜向右上方由静止开始匀加速飞行,经时间t后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,下列说法中正确的是( )| A. | 加速时动力的大小等于mg | |
| B. | 加速与减速时的加速度大小之比为2:$\sqrt{3}$ | |
| C. | 加速与减速过程发生的位移大小之比为1:2 | |
| D. | 减速飞行时间t后速度为零 |
1. 如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则球A、B的质量之比和杆对A、B的弹力之比分别为( )
如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则球A、B的质量之比和杆对A、B的弹力之比分别为( )
 如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则球A、B的质量之比和杆对A、B的弹力之比分别为( )
如图所示,一根轻质细绳跨过定滑轮连接两个小球A、B,它们都穿在一根光滑的竖直杆上,不计细绳与滑轮之间的摩擦,当两球平衡时OA绳与水平方向的夹角为60°,OB绳与水平方向的夹角为30°,则球A、B的质量之比和杆对A、B的弹力之比分别为( )| A. | $\frac{{m}_{A}}{{m}_{B}}$=$\frac{\sqrt{3}}{1}$ | B. | $\frac{{m}_{A}}{{m}_{B}}$=$\frac{\sqrt{3}}{3}$ | C. | $\frac{{F}_{NA}}{{F}_{NB}}$=$\frac{\sqrt{3}}{3}$ | D. | $\frac{{F}_{NA}}{{F}_{NB}}$=$\frac{\sqrt{3}}{2}$ |
11.某物体做匀变速直线运动,其位移与时间的关系为x=0.5t+t2(m),则当物体的速度为3m/s时,物体已运动的时间为( )
| A. | 1.25 s | B. | 2.5 s | C. | 3 s | D. | 6 s |
18. 平行板电容器的两板A、B接于电池两极,一个带正电小球用绝缘细线悬挂在电容器内部,闭合电键S,电容器充电,这时悬线偏离竖直方向夹角为θ,如图所示,那么( )
平行板电容器的两板A、B接于电池两极,一个带正电小球用绝缘细线悬挂在电容器内部,闭合电键S,电容器充电,这时悬线偏离竖直方向夹角为θ,如图所示,那么( )
 平行板电容器的两板A、B接于电池两极,一个带正电小球用绝缘细线悬挂在电容器内部,闭合电键S,电容器充电,这时悬线偏离竖直方向夹角为θ,如图所示,那么( )
平行板电容器的两板A、B接于电池两极,一个带正电小球用绝缘细线悬挂在电容器内部,闭合电键S,电容器充电,这时悬线偏离竖直方向夹角为θ,如图所示,那么( )| A. | 保持电键S闭合,将A板稍向B板靠近,则θ增大 | |
| B. | 保持电键S闭合,将A板稍向上移,则θ减小 | |
| C. | 电键S断开,将A板稍向B板靠近,则θ不变 | |
| D. | 电键S断开,将A板稍向上移,则θ减小 |
13.一直流电动机正常工作时两端的电压为U,通过的电流为I,电动机线圈的电阻为r.该电动机正常工作时,下列说法正确的是( )
| A. | 电动机消耗的电功率为IU | B. | 电动机的输出功率为IU-I2r | ||
| C. | 电动机的发热功率为$\frac{{U}^{2}}{r}$ | D. | I、U、r三个量间满足I=$\frac{U}{r}$ |