题目内容
8.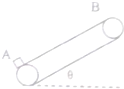 多工厂的流水线上安装有传送带,用传送带传送工件,可以大大提高工作效率.传送带以恒定的速率v=2m/s运送质量为m=0.5kg的工件,工件从A位置放到传送带上,它的初速度忽略不计.工件与传送带之间的动摩擦因数$μ=\frac{\sqrt{3}}{2}$,传送带与水平方向夹角是θ=30°,传送带AB长度是l=16.8m;每当前一个工件在传送带上停止相对滑动时后一个工件立即放到传送带上,取g=10m/s2,求:
多工厂的流水线上安装有传送带,用传送带传送工件,可以大大提高工作效率.传送带以恒定的速率v=2m/s运送质量为m=0.5kg的工件,工件从A位置放到传送带上,它的初速度忽略不计.工件与传送带之间的动摩擦因数$μ=\frac{\sqrt{3}}{2}$,传送带与水平方向夹角是θ=30°,传送带AB长度是l=16.8m;每当前一个工件在传送带上停止相对滑动时后一个工件立即放到传送带上,取g=10m/s2,求:(1)工件放到传送带后经多长时间停止相对滑动?
(2)在正常运行状态下传送带上相邻工件间的距离?
(3)在工件加速阶段传送带上摩擦力对每个工件做的功?
(4)在工件加速阶段传送带克服摩擦力做的功?
(5)每个工件与传送带之间由于摩擦产生的内能?
(6)正常工作中传送带上一直有多少个工件在运动?
(7)传送带克服摩擦力做功的功率?
分析 (1)根据牛顿第二定律求出工件上滑的加速度,结合速度时间公式求出工件与传送带相对静止所需的时间;
(2)工件放上传送带后先做匀加速直线运动,速度达到传送带速度后,做匀速直线运动,结合运动学公式求出在正常运行状态下传送带上相邻工件间的距离;
(3、4)工件在匀加速运动阶段,滑动摩擦力做正功,结合匀加速运动的位移求出摩擦力对每个工件做功的大小以及传送带克服摩擦力做的功;
(5)根据运动学公式求出工件和传送带之间的相对运动位移大小,结合Q=fx相对求出摩擦产生的内能;
(6、7)根据相邻工件间的距离求出传送带上工件的个数,从而得出传送带需施加的摩擦力大小,结合P=fv求出传送带克服摩擦力做功的功率.
解答 解:(1)根据牛顿第二定律得:μmgcosθ-mgsinθ=ma,
解得:a=μgcosθ-gsinθ=$\frac{\sqrt{3}}{2}$×10×$\frac{\sqrt{3}}{2}$-10×$\frac{1}{2}$m/s2=2.5m/s2;
根据v=at得工件放到传送带后相对静止所经历的时间为:t=$\frac{v}{a}=\frac{2}{2.5}$s=0.8s.
(2)停止滑动前,工件相对地移动的距离为:l1=$\frac{1}{2}$at2=$\frac{1}{2}$×2.5×0.82=0.8m,
则在正常运行状态下传送带上相邻工件间的距离为:△l=vt+$\frac{1}{2}$at2-$\frac{1}{2}$at2=vt=2×0.8m=1.6m,
(3)在工件加速阶段传送带上摩擦力对每个工件做的功为:W1=f1l1=μmgcosθ•l1=$\frac{\sqrt{3}}{2}$×5×$\frac{\sqrt{3}}{2}$×0.8=3J,
(4)在工件加速阶段传送带的位移为:x2=vt=1.6m,
此过程中,传送带克服摩擦力做的功为:W2=f1x2=6J,
(5)每个工件与传送带之间由于摩擦产生的内能为:Q=f1△s=μmgcosθ(vt-$\frac{1}{2}$vt)=$\frac{15}{4}$×(1.6-0.8)J=3J.
(6)n=$\frac{l}{△l}=\frac{16.8}{1.6}$=10.5,所以正常工作中皮带上共有工件11个工件在运动,
(7)满载时皮带上共有工件11个,其中10个在做匀速直线运动,
f总=f1+10f2=28.75N
所以传送带克服摩擦力做功的功率P=f总v=28.75×2=57.5W.
答:(1)工件放到传送带后经0.8s时间停止相对滑动;
(2)在正常运行状态下传送带上相邻工件间的距离为1.6m;
(3)在工件加速阶段传送带上摩擦力对每个工件做的功为3J;
(4)在工件加速阶段传送带克服摩擦力做的功为6J;
(5)每个工件与传送带之间由于摩擦产生的内能为3J;
(6)正常工作中传送带上一直有11个工件在运动;
(7)传送带克服摩擦力做功的功率为57.5W.
点评 本题一方面要分析工件的运动情况,由牛顿第二定律和运动学公式结合求解相对位移,即可求出摩擦产生的热量,另一方面要分析能量如何转化,难度适中.

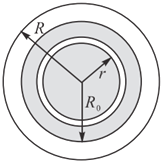 设定地球是一个质量均匀分布的球体,己知质量分布均匀的球壳对其内部物体的引力为零.如图所示,有科学家设想在地球内部修建一条半径为r的环形轨道,在环形轨道内发射一颗人造“地星”A,人造“地星”仅在万有引力作用下做匀速圆周运动.另在地球上空发射一颗轨道半径为R的人造地球卫星B.己知地球半径为Ro,则下列关于“地星”A与卫星B运动的向心加速度大小、线速度大小、角速度、周期之比正确的是( )
设定地球是一个质量均匀分布的球体,己知质量分布均匀的球壳对其内部物体的引力为零.如图所示,有科学家设想在地球内部修建一条半径为r的环形轨道,在环形轨道内发射一颗人造“地星”A,人造“地星”仅在万有引力作用下做匀速圆周运动.另在地球上空发射一颗轨道半径为R的人造地球卫星B.己知地球半径为Ro,则下列关于“地星”A与卫星B运动的向心加速度大小、线速度大小、角速度、周期之比正确的是( )| A. | $\frac{{a}_{A}}{{a}_{B}}$=($\frac{R}{r}$)2 | B. | $\frac{{v}_{A}}{{v}_{B}}$=$\frac{r}{{R}_{0}}$$\sqrt{\frac{R}{{R}_{0}}}$ | C. | $\frac{{ω}_{A}}{{ω}_{B}}$=$\frac{R}{{R}_{0}}$$\sqrt{\frac{R}{{R}_{0}}}$ | D. | $\frac{{T}_{A}}{{T}_{B}}$=$\frac{R}{r}$$\sqrt{\frac{R}{r}}$ |
 某同学为研究电动机在启动和工作过程中电流的变化情况,设计如图所示的电路,则下列说法中正确的是( )
某同学为研究电动机在启动和工作过程中电流的变化情况,设计如图所示的电路,则下列说法中正确的是( )| A. | 电动机启动时的电流小于正常工作时的电流 | |
| B. | 电动机有负载时的电流小于空载时的电流 | |
| C. | 若增大电动机的负载,则电流增大 | |
| D. | 由于电动机内阻不变,因此电流与电动机的负载无关 |
 如图所示,质量分别为ma、mb的两物体a和b,通过一根跨过定滑轮的轻绳连接在一起,其中物体b放在光滑斜面上,开始时两物体均处于静止状态.不计绳与滑轮间的摩擦.当两物体以大小相同的速度v0匀速运动时.下列说法正确的是( )
如图所示,质量分别为ma、mb的两物体a和b,通过一根跨过定滑轮的轻绳连接在一起,其中物体b放在光滑斜面上,开始时两物体均处于静止状态.不计绳与滑轮间的摩擦.当两物体以大小相同的速度v0匀速运动时.下列说法正确的是( )| A. | 物体a的质量一定等于物体b的质量 | |
| B. | 物体a的质量一定小于物体b的质量 | |
| C. | 运动过程中,物体a的机械能减小,物体b的机械能增加 | |
| D. | 运动过程中,物体a的机械能守恒,物体b的机械能守恒 |

| A. | $\frac{3}{4}$倍 | B. | $\frac{4}{3}$倍 | C. | $\frac{3}{2}$倍 | D. | 2倍 |
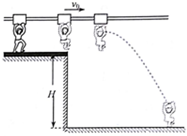 某电视娱乐节目“快乐向前冲”的场地设施如图.足够长的水平滑杆上装有可沿杆自由滑动的悬挂器,悬挂器与滑杆的动摩擦因数为μ=0.2,选手在离地高H=5m的平台上,抓住悬挂器经过一定距离的助跑,可获得初速度并滑离平台.为了落在地面合适的位置,选手必须做好判断,在合适的时机位置放开悬挂器,g取10m/s2.
某电视娱乐节目“快乐向前冲”的场地设施如图.足够长的水平滑杆上装有可沿杆自由滑动的悬挂器,悬挂器与滑杆的动摩擦因数为μ=0.2,选手在离地高H=5m的平台上,抓住悬挂器经过一定距离的助跑,可获得初速度并滑离平台.为了落在地面合适的位置,选手必须做好判断,在合适的时机位置放开悬挂器,g取10m/s2. 一棱镜的截面为直角三角形ABC,其中∠A=30°,在此截面所在的平面内,一条光线以i=45°的入射角从AC边的中点M射入棱镜,经过一次折射和全反射后垂直于BC边从E点射出,求:
一棱镜的截面为直角三角形ABC,其中∠A=30°,在此截面所在的平面内,一条光线以i=45°的入射角从AC边的中点M射入棱镜,经过一次折射和全反射后垂直于BC边从E点射出,求: 一定质量的理想气体经历了如图所示的ABCDA循环,p1、p2、V1、V2均为已知量.已知A状态的温度为T0,求:
一定质量的理想气体经历了如图所示的ABCDA循环,p1、p2、V1、V2均为已知量.已知A状态的温度为T0,求: