题目内容
20.A、B两个同样的人造卫星,用不同的火箭发射,它们都成功地环绕地球做圆周运动,A的轨道半径是B的2倍,则A卫星运动的线速度是B卫星运动的线速度的$\frac{\sqrt{2}}{2}$倍,A卫星运动的周期是B卫星的$2\sqrt{2}$.分析 两颗质量相等的人造卫星绕同一个中心天体做圆周运动,靠万有引力提供向心力,根据$F=G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m\frac{4{π}^{2}r}{{T}^{2}}$列式求解即可.
解答 解:根据万有引力提供向心力有:F=$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}=m\frac{4{π}^{2}r}{{T}^{2}}=ma$,
解得:v=$\sqrt{\frac{GM}{r}}$,T=2$π\sqrt{\frac{{r}^{3}}{GM}}$,
A的轨道半径是B的2倍,即rA=2rB,
则 $\frac{{v}_{A}}{{v}_{B}}=\sqrt{\frac{{r}_{B}}{{r}_{A}}}=\frac{\sqrt{2}}{2}$,$\frac{{T}_{A}}{{T}_{B}}=\sqrt{\frac{{{r}_{A}}^{3}}{{{r}_{B}}^{3}}}=2\sqrt{2}$.
故答案为:$\frac{\sqrt{2}}{2}$;$2\sqrt{2}$.
点评 解决本题的关键掌握万有引力提供向心力,会根据轨道半径比较线速度、周期、向心加速度等,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.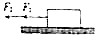 如图所示,一质点静止在光滑水平面上,从某时刻开始同时受到两个水平方向的力F1、F2作用,F1、F2方向都和质点运动方向相反,其中F1的功率不变,大小为P,F2=kv(k为比例系数,v为质点的瞬时速度).则质点在以后运动过程中.加速度大小的可能为( )
如图所示,一质点静止在光滑水平面上,从某时刻开始同时受到两个水平方向的力F1、F2作用,F1、F2方向都和质点运动方向相反,其中F1的功率不变,大小为P,F2=kv(k为比例系数,v为质点的瞬时速度).则质点在以后运动过程中.加速度大小的可能为( )
 如图所示,一质点静止在光滑水平面上,从某时刻开始同时受到两个水平方向的力F1、F2作用,F1、F2方向都和质点运动方向相反,其中F1的功率不变,大小为P,F2=kv(k为比例系数,v为质点的瞬时速度).则质点在以后运动过程中.加速度大小的可能为( )
如图所示,一质点静止在光滑水平面上,从某时刻开始同时受到两个水平方向的力F1、F2作用,F1、F2方向都和质点运动方向相反,其中F1的功率不变,大小为P,F2=kv(k为比例系数,v为质点的瞬时速度).则质点在以后运动过程中.加速度大小的可能为( )| A. | $\frac{\sqrt{Pk}}{2m}$ | B. | $\frac{\sqrt{Pk}}{m}$ | C. | $\frac{3\sqrt{Pk}}{m}$ | D. | $\frac{4\sqrt{Pk}}{m}$ |
12. 在直角坐标系的第一、四象限内有一横截面为半圆形的柱状玻璃砖MNP,两束平行于x轴且与x轴等距离的可见单色光a、b,从空气中垂直y轴射入玻璃砖中,在MNP面上发生反射和折射的实际情况如图所示,由此可知( )
在直角坐标系的第一、四象限内有一横截面为半圆形的柱状玻璃砖MNP,两束平行于x轴且与x轴等距离的可见单色光a、b,从空气中垂直y轴射入玻璃砖中,在MNP面上发生反射和折射的实际情况如图所示,由此可知( )
 在直角坐标系的第一、四象限内有一横截面为半圆形的柱状玻璃砖MNP,两束平行于x轴且与x轴等距离的可见单色光a、b,从空气中垂直y轴射入玻璃砖中,在MNP面上发生反射和折射的实际情况如图所示,由此可知( )
在直角坐标系的第一、四象限内有一横截面为半圆形的柱状玻璃砖MNP,两束平行于x轴且与x轴等距离的可见单色光a、b,从空气中垂直y轴射入玻璃砖中,在MNP面上发生反射和折射的实际情况如图所示,由此可知( )| A. | a光在玻璃砖内的频率比在空气中的小 | |
| B. | a光的频率比b光的小 | |
| C. | a光的折射率大于b光的折射率 | |
| D. | 在玻璃砖内a光的传播速度比c小 | |
| E. | 相同条件下进行双缝干涉实验,a光的条纹间距比b光的小 |
 如图所示,同种介质中有两列简谐横波相向传播,实线表示的波向x轴正方向传播,虚线表示的波向x轴负方向传播,在t=0时刻,两列波已在2m≤x≤4m范围内相遇.已知波的频率为8Hz,两列波的振幅均为1cm,两列波相遇后,x=3m处质点的振幅为2cm.
如图所示,同种介质中有两列简谐横波相向传播,实线表示的波向x轴正方向传播,虚线表示的波向x轴负方向传播,在t=0时刻,两列波已在2m≤x≤4m范围内相遇.已知波的频率为8Hz,两列波的振幅均为1cm,两列波相遇后,x=3m处质点的振幅为2cm. 多工厂的流水线上安装有传送带,用传送带传送工件,可以大大提高工作效率.传送带以恒定的速率v=2m/s运送质量为m=0.5kg的工件,工件从A位置放到传送带上,它的初速度忽略不计.工件与传送带之间的动摩擦因数$μ=\frac{\sqrt{3}}{2}$,传送带与水平方向夹角是θ=30°,传送带AB长度是l=16.8m;每当前一个工件在传送带上停止相对滑动时后一个工件立即放到传送带上,取g=10m/s2,求:
多工厂的流水线上安装有传送带,用传送带传送工件,可以大大提高工作效率.传送带以恒定的速率v=2m/s运送质量为m=0.5kg的工件,工件从A位置放到传送带上,它的初速度忽略不计.工件与传送带之间的动摩擦因数$μ=\frac{\sqrt{3}}{2}$,传送带与水平方向夹角是θ=30°,传送带AB长度是l=16.8m;每当前一个工件在传送带上停止相对滑动时后一个工件立即放到传送带上,取g=10m/s2,求:




 如图所示,右端开口的绝缘、绝热圆柱形汽缸放置在水平地面上,容积为V,汽缸内部被绝热活塞M和导热性能良好的活塞N分成三个相等的部分,左边两部分分别封闭气体A和B,两活塞均与汽缸接触良好,忽略一切摩擦,汽缸左边有加热装置,可对气体A缓慢加热,初始状态温度为T0,大气压强为P0
如图所示,右端开口的绝缘、绝热圆柱形汽缸放置在水平地面上,容积为V,汽缸内部被绝热活塞M和导热性能良好的活塞N分成三个相等的部分,左边两部分分别封闭气体A和B,两活塞均与汽缸接触良好,忽略一切摩擦,汽缸左边有加热装置,可对气体A缓慢加热,初始状态温度为T0,大气压强为P0