题目内容
5．
一定质量的理想气体经历了如图所示的ABCDA循环，p1、p2、V1、V2均为已知量．已知A状态的温度为T0，求：①C状态的温度T；
②完成一个循环，气体与外界热交换的热量Q．
分析 ①根据图示图象判断出气体状态变化过程，然后应用查理定律与盖吕萨克定律求出气体的温度；
②根据图示图象求出整个过程气体对外做功，然后应用热力学第一定律求出气体与外界交换的热量．
解答 解：①由图示图象可知，从C到D过程为等容变化，由查理定律得：$\frac{{p}_{2}}{T}$=$\frac{{p}_{1}}{{T}_{D}}$，
由图示图象可知，从D到A过程为等压变化，由盖吕萨克定律得：$\frac{{V}_{2}}{{T}_{D}}$=$\frac{{V}_{1}}{{T}_{0}}$，
解得：T=$\frac{{p}_{2}{V}_{2}{T}_{0}}{{p}_{1}{V}_{1}}$；
②由C到D过程与由A到B过程气体体积不变，气体不做功，
从B到C过程气体对外做功，WBC=-p2（V2-V1），
从D到A过程外界对气体做功，WDA=p1（V2-V1），
对全过程气体做功：W=WBC+WDA=（p1-p2）（V2-V1），
整个过程气体温度不变，△U=0，
由热力学第一定律得：△U=W+Q，
则：Q=△U-W=（p2-p1）（V2-V1）＞0，气体吸热；
答：①C状态的温度T为$\frac{{p}_{2}{V}_{2}{T}_{0}}{{p}_{1}{V}_{1}}$；
②完成一个循环，气体从外界吸收的热量为：（p2-p1）（V2-V1）．
点评 本题考查了求气体的温度与气体与外界交换的热量，分析清楚图示图象、分析清楚气体状态变化过程是解题的前提与关键；应用查理定律、盖吕萨克定律与热力学第一定律可以解题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
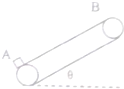多工厂的流水线上安装有传送带，用传送带传送工件，可以大大提高工作效率．传送带以恒定的速率v=2m/s运送质量为m=0.5kg的工件，工件从A位置放到传送带上，它的初速度忽略不计．工件与传送带之间的动摩擦因数$μ=\frac{\sqrt{3}}{2}$，传送带与水平方向夹角是θ=30°，传送带AB长度是l=16.8m；每当前一个工件在传送带上停止相对滑动时后一个工件立即放到传送带上，取g=10m/s2，求：
如图所示，在球形烧瓶上连一根水平玻璃管，管中装有一小段水银柱把瓶中气体与外界的大气隔开，将烧瓶从室温情况下浸人热水中，可以看到此时水平玻璃管中的木银柱将向右移动（选填“向左”、“向右”或“不”）．在这个实验中，烧瓶中气体初、末状态参量的变化是：压强不变，温度升高，体积增加．
10．
如图，两端封闭的玻璃管竖直放置，内有一段水银柱将空气柱分为两段，两段气柱的质量、温度均相同．开始时玻璃管静止，后以恒定向上的加速度运动，与静止时相比，稳定后上、下气柱压强变化量的大小分别为△p上、△p下，不计气体温度的变化，则相对玻璃管（ ）
如图，两端封闭的玻璃管竖直放置，内有一段水银柱将空气柱分为两段，两段气柱的质量、温度均相同．开始时玻璃管静止，后以恒定向上的加速度运动，与静止时相比，稳定后上、下气柱压强变化量的大小分别为△p上、△p下，不计气体温度的变化，则相对玻璃管（ ）| A． | 水银柱向上移动，且△p上＞△p下 | B． | 水银柱向上移动，且△p上＜△p下 | ||
| C． | 水银柱向下移动，且△p上＜△p下 | D． | 水银柱向下移动，且△p上＞△p下 |
如图所示，右端开口的绝缘、绝热圆柱形汽缸放置在水平地面上，容积为V，汽缸内部被绝热活塞M和导热性能良好的活塞N分成三个相等的部分，左边两部分分别封闭气体A和B，两活塞均与汽缸接触良好，忽略一切摩擦，汽缸左边有加热装置，可对气体A缓慢加热，初始状态温度为T0，大气压强为P0
在做“研究平抛运动”实验时，让小球多次沿同一轨道运动，通过描点法画出小球平抛运动的轨迹．