题目内容
14. 如图所示.一只一端封闭的粗细均匀的玻璃管开口向上,用一段长度为h的水银柱密封一定童的理想气体,玻璃管静止时气柱长度为L(图甲).现将该玻璃管从倾角为θ的斜面顶端由静止释放,并沿斜面向下运动(图乙).已知玻璃管与斜面之间的动摩擦因数为μ.水银密度为ρ.重力加速度为g,大气压强为p0,气体温度不变,斜面足够长.求:
如图所示.一只一端封闭的粗细均匀的玻璃管开口向上,用一段长度为h的水银柱密封一定童的理想气体,玻璃管静止时气柱长度为L(图甲).现将该玻璃管从倾角为θ的斜面顶端由静止释放,并沿斜面向下运动(图乙).已知玻璃管与斜面之间的动摩擦因数为μ.水银密度为ρ.重力加速度为g,大气压强为p0,气体温度不变,斜面足够长.求:(i)玻璃管竖直静止时,气体的压强;
(ii)玻璃管在斜面上运动时,玻璃管内气柱的长度.
分析 (1)对水银柱进行受力分析,结合共点力的平衡即可求出气体的压强;
(2)玻璃管沿斜面运动的过程中做匀加速直线运动,设出加速度,将受力分析与牛顿第二定律结合,求出水银柱的加速度的表达式,进而求出气体的压强,最后由玻意耳定律求出气体的长度.
解答 解:(1)设玻璃管竖直放置时气体的压强为P1,水银柱受到重力、大气压力与气体对水银柱的向上的压力,由力的平衡得:
P0S+mg=P1S ①
又:mg=ρV=ρSh ②
联立①②得:P1=P0+ρgh ③
(2)玻璃管沿斜面运动的过程中做匀加速直线运动,设加速度为a,根据牛顿第二定律得:
mgsinθ-μmgcosθ=ma
得:a=g(sinθ-μcosθ)
设玻璃管在斜面上运动的过程中气体的压强是P2,气柱的长度是L′,研究水银柱的受力的情况,根据牛顿第二定律得:
P0S+mgsinθ-P2S=ma
解得:P2=P0+ρgh•μcosθ
由玻意耳定律:P1L=P2L′
解得:$L′=\frac{({P}_{0}+ρgh)L}{{P}_{0}+μρgh•cosθ}$
答:(i)玻璃管竖直静止时,气体的压强是P0+ρgh;
(ii)玻璃管在斜面上运动时,玻璃管内气柱的长度$\frac{({P}_{0}+ρgh)L}{{P}_{0}+μρgh•cosθ}$.
点评 利用理想气体状态方程解题,关键是正确选取状态,明确状态参量,尤其是正确求解被封闭气体的压强,这是热学中的重点知识,要加强训练,加深理解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.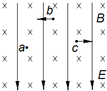 如图所示,匀强电场E竖直向下,匀强磁场B垂直纸面向里.现有三个带有等量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做匀速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )
如图所示,匀强电场E竖直向下,匀强磁场B垂直纸面向里.现有三个带有等量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做匀速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )
 如图所示,匀强电场E竖直向下,匀强磁场B垂直纸面向里.现有三个带有等量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做匀速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )
如图所示,匀强电场E竖直向下,匀强磁场B垂直纸面向里.现有三个带有等量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做匀速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )| A. | 三个油滴都带正电 | |
| B. | 油滴a一定是做顺时针方向的圆周运动 | |
| C. | 三个油滴中b的质量最大 | |
| D. | 三个油滴中c的质量最大 |
5. 一质量为2kg的物体沿水平面作直线运动,其v-t图象如图所示,下列选项中正确的是( )
一质量为2kg的物体沿水平面作直线运动,其v-t图象如图所示,下列选项中正确的是( )
 一质量为2kg的物体沿水平面作直线运动,其v-t图象如图所示,下列选项中正确的是( )
一质量为2kg的物体沿水平面作直线运动,其v-t图象如图所示,下列选项中正确的是( )| A. | 前6 s内,合外力对物体做功为64 J | |
| B. | 在3 s-5 s内,质点的平均速度为4 m/s | |
| C. | 在前6 s内,质点离出发点的最远距离为28 m | |
| D. | 质点在第5 s末的加速度为0 |
9. A、B两物体的质量之比mA:mB=2:1,它们以相同的初速度v0在水平面上做匀减速直线运动,直到停止,其速度图象如图所示.那么,A、B两物体所受摩擦阻力之比FA:FB与A、B两物体克服摩擦阻力做的功之比WA:WB分别为( )
A、B两物体的质量之比mA:mB=2:1,它们以相同的初速度v0在水平面上做匀减速直线运动,直到停止,其速度图象如图所示.那么,A、B两物体所受摩擦阻力之比FA:FB与A、B两物体克服摩擦阻力做的功之比WA:WB分别为( )
 A、B两物体的质量之比mA:mB=2:1,它们以相同的初速度v0在水平面上做匀减速直线运动,直到停止,其速度图象如图所示.那么,A、B两物体所受摩擦阻力之比FA:FB与A、B两物体克服摩擦阻力做的功之比WA:WB分别为( )
A、B两物体的质量之比mA:mB=2:1,它们以相同的初速度v0在水平面上做匀减速直线运动,直到停止,其速度图象如图所示.那么,A、B两物体所受摩擦阻力之比FA:FB与A、B两物体克服摩擦阻力做的功之比WA:WB分别为( )| A. | 2:1 4:1 | B. | 4:1 2:1 | C. | 1:4 1:2 | D. | 1:2 1:4 |
3.关于重力的大小,下列说法不正确的是( )
| A. | 物体的重力跟质量成正比 | |
| B. | g=9.8N/kg表示质量为1kg的物体所受重力是9.8N | |
| C. | 放在斜面上的物体比在平面上受的重力小 | |
| D. | 在地面附近,物体静止时与运动时,其重力大小是不变的 |
4.已知万有引力恒量,在以下各组数椐中,根椐哪几组可以测地球质量( )
| A. | 地球绕太阳运行的周期及太阳与地球的距离 | |
| B. | 月球绕地球运行的周期及月球到地球表面的距离 | |
| C. | 地球自转周期及近地卫星离地球的距离 | |
| D. | 若不考虑地球自转,地球半径及地球表面的重力加速度 |
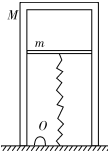 一汽缸竖直放在水平地面上,缸体质量M=10kg,活塞质量m=4kg,活塞横截面积S=2×10-3m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面有气孔O与外界相通,大气压强P0=1.0×105Pa;活塞下面与劲度系数k=2×103M/m的轻弹簧相连;当汽缸内气体温度为127℃时弹簧为自然长度,此时缸内气柱长度L1=20cm,g取10m/s2,缸体始终竖直,活塞不漏气且与缸壁无摩擦.
一汽缸竖直放在水平地面上,缸体质量M=10kg,活塞质量m=4kg,活塞横截面积S=2×10-3m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面有气孔O与外界相通,大气压强P0=1.0×105Pa;活塞下面与劲度系数k=2×103M/m的轻弹簧相连;当汽缸内气体温度为127℃时弹簧为自然长度,此时缸内气柱长度L1=20cm,g取10m/s2,缸体始终竖直,活塞不漏气且与缸壁无摩擦. 在方向水平向右,大小E=1×104N/C的匀强电场中,用细线将质量m=4×10-3kg的带电小球P悬挂在O点,小球静止时细线与竖直方向夹角θ=37°(已知sin37°=0.6,cos37°=0.8).求:
在方向水平向右,大小E=1×104N/C的匀强电场中,用细线将质量m=4×10-3kg的带电小球P悬挂在O点,小球静止时细线与竖直方向夹角θ=37°(已知sin37°=0.6,cos37°=0.8).求: