题目内容
12. 如图所示,内壁光滑半径大小为R的圆轨道竖直固定在桌面上,一个质量为m的小球静止在轨道底部A点.现用小锤沿水平方向快速击打小球,击打后迅速移开,使小球沿轨道在竖直面内运动.当小球回到A点时,再次用小锤沿运动方向击打小球,通过两次击打,小球才能运动到圆轨道的最高点.已知小球在运动过程中始终未脱离轨道,在第一次击打过程中小锤对小球做功W1,第二次击打过程中小锤对小球做功W2.设先后两次击打过程中小锤对小球做功全部用来增加小球的动能,则$\frac{{W}_{1}}{{W}_{2}}$的值可能是( )
如图所示,内壁光滑半径大小为R的圆轨道竖直固定在桌面上,一个质量为m的小球静止在轨道底部A点.现用小锤沿水平方向快速击打小球,击打后迅速移开,使小球沿轨道在竖直面内运动.当小球回到A点时,再次用小锤沿运动方向击打小球,通过两次击打,小球才能运动到圆轨道的最高点.已知小球在运动过程中始终未脱离轨道,在第一次击打过程中小锤对小球做功W1,第二次击打过程中小锤对小球做功W2.设先后两次击打过程中小锤对小球做功全部用来增加小球的动能,则$\frac{{W}_{1}}{{W}_{2}}$的值可能是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 第一次击打后球最多到达与球心O等高位置,根据功能关系列式;两次击打后可以到轨道最高点,再次根据功能关系列式;最后联立求解即可.
解答 解:第一次击打后球最多到达与球心O等高位置,根据功能关系,有:
W1≤mgR…①
两次击打后可以到轨道最高点,根据功能关系,有:
W1+W2-2mgR=$\frac{1}{2}m{v}^{2}$…②
在最高点,有:
mg+N=m$\frac{{v}^{2}}{R}$≥mg…③
联立①②③解得:
W1≤mgR
W2≥$\frac{3}{2}$mgR
故$\frac{{W}_{1}}{{W}_{2}}≤$$\frac{2}{3}$
故AB正确,CD错误;
故选:AB.
点评 本题关键是抓住临界状态,然后结合功能关系和牛顿第二定律列式分析,不难.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
2. 小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路,不计电路的其他电阻.下列说法正确的是( )
小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路,不计电路的其他电阻.下列说法正确的是( )
 小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路,不计电路的其他电阻.下列说法正确的是( )
小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动,产生的感应电动势与时间呈正弦函数关系,如图所示.此线圈与一个R=10Ω的电阻构成闭合电路,不计电路的其他电阻.下列说法正确的是( )| A. | 交变电流的周期为0.125 s | B. | 交变电流的频率为8 Hz | ||
| C. | 交变电流的有效值为$\sqrt{2}$ A | D. | 交变电流的最大值为4 A |
17.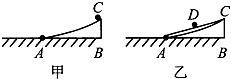 如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )
如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )
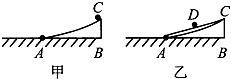 如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )
如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )| A. | v1>v2,t1>t2 | B. | v1>v2,t1=t2 | C. | v1>v2,t1<t2 | D. | v1=v2,t1=t2 |
1. 一列横波在t=0时的波形如图所示,C点此时向下运动,A、B两质点间距为8m,B、C两质点在平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,则该波的波速可能为( )
一列横波在t=0时的波形如图所示,C点此时向下运动,A、B两质点间距为8m,B、C两质点在平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,则该波的波速可能为( )
 一列横波在t=0时的波形如图所示,C点此时向下运动,A、B两质点间距为8m,B、C两质点在平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,则该波的波速可能为( )
一列横波在t=0时的波形如图所示,C点此时向下运动,A、B两质点间距为8m,B、C两质点在平衡位置的间距为3m,当t=1s时,质点C恰好通过平衡位置,则该波的波速可能为( )| A. | $\frac{1}{3}$m/s | B. | 3m/s | C. | 15m/s | D. | 27m/s |
2.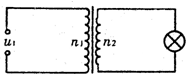 如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
 如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )
如图所示,理想变压器的原、副线圈匝数比n1:n2=20:1,原线圈接u1=UmsinωtV的正弦交变电压,副线圈中标有“10V 100W”的灯泡正常发光,则( )| A. | Um=200V | B. | Um=200$\sqrt{2}V$ | ||
| C. | 当ωt=$\frac{π}{2}$时,副线圈中的电流为O | D. | 当ωt=π时,副线圈中的电流为O |
 某同学用频闪照相法来研究自由落体运动,图中的数据是前4个曝光位置,小球的第一个曝光位置对应的A点速度是否为零?否(填“是”或“否”).若频闪时间间隔为0.04s,则vc=0.4m/s,小球自由落体运动的加速度为10m/s2.
某同学用频闪照相法来研究自由落体运动,图中的数据是前4个曝光位置,小球的第一个曝光位置对应的A点速度是否为零?否(填“是”或“否”).若频闪时间间隔为0.04s,则vc=0.4m/s,小球自由落体运动的加速度为10m/s2. 1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.在D盒中心A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U.
1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.在D盒中心A处粒子源产生的粒子,质量为m、电荷量为+q,在加速器中被加速,加速电压为U. 如图所示,有一内阻未知(约20kΩ~30kΩ)的直流电压表,某同学想利用一个多用电表的欧姆挡测量该电压表的内阻,他从多用电表刻度盘上读出电阻刻度盘的中间值为25.
如图所示,有一内阻未知(约20kΩ~30kΩ)的直流电压表,某同学想利用一个多用电表的欧姆挡测量该电压表的内阻,他从多用电表刻度盘上读出电阻刻度盘的中间值为25.