题目内容
17.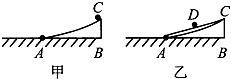 如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )
如图甲所示,AC是一段光滑的圆弧形面,圆弧的半径为1.00m,圆弧形面与水平面相切于A点,弧长AC为4.0cm.现将一小球在弧AC的顶点C由静止释放,此物体沿弧AC运动至最低端A点时的速度大小为v1,所用时间为t1.如图乙所示,再以A、C为端点作光滑的斜面,将此小球在斜面AC的中点D处由静止释放,此物体运动到A点时的速度大小为v2,所用时间为t2.则有( )| A. | v1>v2,t1>t2 | B. | v1>v2,t1=t2 | C. | v1>v2,t1<t2 | D. | v1=v2,t1=t2 |
分析 由于CO的弧长远小于圆弧的半径,所以小球的运动可视为简谐运动(单摆运动),根据周期公式T=2π$\sqrt{\frac{L}{g}}$,比较时间.根据动能定理比较到达O点的速度.
解答 解:小球运动过程机械能守恒,由机械能守恒定律得:mg△h=$\frac{1}{2}$mv2-0,由图示可知,C点的△h大,所以从C点释放到达O点的速度大,即:v1>v2;
甲图中,小球在圆弧上的运动可视为简谐运动(单摆运动),小球从C到A的运动时间等于单摆的$\frac{1}{4}$周期,t1=$\frac{1}{4}$T=$\frac{π}{2}$$\sqrt{\frac{R}{g}}$=$\frac{π}{2}$$\sqrt{\frac{1}{g}}$s,
乙图中,斜面倾角θ=$\frac{1}{2}$×$\frac{0.04}{1}$=0.02,小球下滑的加速度:a=gisnθ≈gθ,位移:0.02=$\frac{1}{2}$at22,t2=$\sqrt{\frac{2}{g}}$s,则t1>t2;
故选:A.
点评 解决本题的关键掌握单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$,以及能够熟练运用动能定理.

练习册系列答案
相关题目
7.下列关于加速度和速度的说法错误的是( )
| A. | 物体运动的加速度等于0,而速度却在增加 | |
| B. | 两物体相比,一个物体的速度变化量大,而加速度却比较小 | |
| C. | 物体具有向东的加速度,而速度的方向却向西 | |
| D. | 物体做直线运动,后一阶段的加速度比前一阶段小,但速度却比前一阶段大 |
5.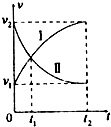 从同一地点同时开始沿同一直线运动的两个物体I、II的速度图象如图所示,在0~t2时间内,下列说法中正确的是( )
从同一地点同时开始沿同一直线运动的两个物体I、II的速度图象如图所示,在0~t2时间内,下列说法中正确的是( )
 从同一地点同时开始沿同一直线运动的两个物体I、II的速度图象如图所示,在0~t2时间内,下列说法中正确的是( )
从同一地点同时开始沿同一直线运动的两个物体I、II的速度图象如图所示,在0~t2时间内,下列说法中正确的是( )| A. | Ⅰ、Ⅱ两个物体在t1时刻相遇 | |
| B. | Ⅰ、Ⅱ两个物体的平均速度大小都是$\frac{{{v_1}+{v_2}}}{2}$ | |
| C. | Ⅰ、Ⅱ两个物体所受的合外力都在不断减小 | |
| D. | Ⅰ物体的加速度不断增大,Ⅱ物体的加速度不断减小 |
12. 如图所示,内壁光滑半径大小为R的圆轨道竖直固定在桌面上,一个质量为m的小球静止在轨道底部A点.现用小锤沿水平方向快速击打小球,击打后迅速移开,使小球沿轨道在竖直面内运动.当小球回到A点时,再次用小锤沿运动方向击打小球,通过两次击打,小球才能运动到圆轨道的最高点.已知小球在运动过程中始终未脱离轨道,在第一次击打过程中小锤对小球做功W1,第二次击打过程中小锤对小球做功W2.设先后两次击打过程中小锤对小球做功全部用来增加小球的动能,则$\frac{{W}_{1}}{{W}_{2}}$的值可能是( )
如图所示,内壁光滑半径大小为R的圆轨道竖直固定在桌面上,一个质量为m的小球静止在轨道底部A点.现用小锤沿水平方向快速击打小球,击打后迅速移开,使小球沿轨道在竖直面内运动.当小球回到A点时,再次用小锤沿运动方向击打小球,通过两次击打,小球才能运动到圆轨道的最高点.已知小球在运动过程中始终未脱离轨道,在第一次击打过程中小锤对小球做功W1,第二次击打过程中小锤对小球做功W2.设先后两次击打过程中小锤对小球做功全部用来增加小球的动能,则$\frac{{W}_{1}}{{W}_{2}}$的值可能是( )
 如图所示,内壁光滑半径大小为R的圆轨道竖直固定在桌面上,一个质量为m的小球静止在轨道底部A点.现用小锤沿水平方向快速击打小球,击打后迅速移开,使小球沿轨道在竖直面内运动.当小球回到A点时,再次用小锤沿运动方向击打小球,通过两次击打,小球才能运动到圆轨道的最高点.已知小球在运动过程中始终未脱离轨道,在第一次击打过程中小锤对小球做功W1,第二次击打过程中小锤对小球做功W2.设先后两次击打过程中小锤对小球做功全部用来增加小球的动能,则$\frac{{W}_{1}}{{W}_{2}}$的值可能是( )
如图所示,内壁光滑半径大小为R的圆轨道竖直固定在桌面上,一个质量为m的小球静止在轨道底部A点.现用小锤沿水平方向快速击打小球,击打后迅速移开,使小球沿轨道在竖直面内运动.当小球回到A点时,再次用小锤沿运动方向击打小球,通过两次击打,小球才能运动到圆轨道的最高点.已知小球在运动过程中始终未脱离轨道,在第一次击打过程中小锤对小球做功W1,第二次击打过程中小锤对小球做功W2.设先后两次击打过程中小锤对小球做功全部用来增加小球的动能,则$\frac{{W}_{1}}{{W}_{2}}$的值可能是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 1 |
6.物理学历史上许多规律的发现或学说的建立,是在科学家之间相互启发、相互印证的过程中应用物理学研究方法逐步完成的.下列说法中符合史实的是( )
| A. | 伽利略在亚里士多德、笛卡尔等科学家关于力与运动关系研究的基础上,运用理想实验和归谬法得出了惯性定律 | |
| B. | 法拉第首先提出了场的概念,并用电场线和磁感线形象地描述电场和磁场 | |
| C. | 卡文迪许巧妙地运用扭秤实验,成功测出了静电力常量的数值 | |
| D. | 牛顿接受了胡克等科学家关于“吸引力与两中心距离的平方成反比”的猜想,运用严密的逻辑推理,建立了万有引力定律 |
 电路如图(甲)所示,定值电阻R=3Ω,电源的路端电压U随电流I的变化图线如图(乙)所示.闭合电键S,求:
电路如图(甲)所示,定值电阻R=3Ω,电源的路端电压U随电流I的变化图线如图(乙)所示.闭合电键S,求:
 质量分别为m1=2kg和m2=1kg的两个小球在光滑的水平面上分速度v1=2m/s、v2=1m/s同向运动并发生对心碰撞,碰后m2被右侧的墙原速弹回,又与m1相碰,碰后两球都静止.求:两球第一次碰后m1球的速度大小.
质量分别为m1=2kg和m2=1kg的两个小球在光滑的水平面上分速度v1=2m/s、v2=1m/s同向运动并发生对心碰撞,碰后m2被右侧的墙原速弹回,又与m1相碰,碰后两球都静止.求:两球第一次碰后m1球的速度大小. 如图所示边长为L的正方形内有磁感应强度为B的匀强磁场,在A、B、C、D、E五点处都开有小孔,不同速度的电子从A孔入射后,在B、C、D都有电子射出.图中α=30°,则求:
如图所示边长为L的正方形内有磁感应强度为B的匀强磁场,在A、B、C、D、E五点处都开有小孔,不同速度的电子从A孔入射后,在B、C、D都有电子射出.图中α=30°,则求: