��Ŀ����
20�� 1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ����D������A������Դ���������ӣ�����Ϊm�������Ϊ+q���ڼ������б����٣����ٵ�ѹΪU��
1932�꣬����˹������˹��Ƴ��˻����������������������Ĺ���ԭ����ͼ��ʾ�����ڸ�����е�D�ν����а뾶ΪR�����м�������С���������Ӵ�����ʱ����Ժ��Բ��ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų�����洹ֱ����D������A������Դ���������ӣ�����Ϊm�������Ϊ+q���ڼ������б����٣����ٵ�ѹΪU����1�������ӵ�2�κ͵�1�ξ�����D�κм���������뾶֮�ȣ�
��2�������ӴӾ�ֹ��ʼ���ٵ����ڴ������ʱ��t��
���� ��1�����������ڴų���������Բ���˶������ݶ��ܶ��������������ṩ�������������뾶����ٵ�ѹ�Ĺ�ϵ���Ӷ��������뾶֮�ȣ�
��2��ͨ��D�κеİ뾶������ӵ�����ٶȣ���϶��ܶ���������ٵĴ�����һ�������ڼ������Σ��Ӷ���֪�ڴų����˶������ڴ�����ȷ�������ӴӾ�ֹ��ʼ���ٵ����ڴ������ʱ�䣮
��� �⣺��1�������ӵ�1�ξ��������İ뾶Ϊr1���ٶ�Ϊv1
qU=$\frac{1}{2}$mv12
qv1B=m$\frac{{v}_{1}^{2}}{{r}_{1}}$
�������Ͻ�ã�r1=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$
ͬ�������ӵ�2�ξ��������İ뾶r2=$\frac{1}{B}\sqrt{\frac{4mU}{q}}$
�� r1��r2=1��$\sqrt{2}$
��2�������ӵ����ڴ���������nȦ����ã�2nqU=$\frac{1}{2}$mv2��
qvB=m$\frac{{v}^{2}}{R}$
T=$\frac{2��m}{qB}$
t=nT
�����ĸ����̵ã�t=$\frac{��B{R}^{2}}{2U}$
�𣺣�1�����ӵ�2�κ͵�1�ξ�����D�κм������Ĺ���뾶֮��Ϊ1��$\sqrt{2}$��
��2�����ӴӾ�ֹ��ʼ���ٵ����ڴ������ʱ��Ϊ$\frac{��B{R}^{2}}{2U}$��
���� �������Ĺؼ����ջ�����������ԭ�������õ糡���ٺʹų�ƫת��֪�������ڴų����˶�����������ٵ糡�ı仯������ȣ�

| A�� | ��ֹ�������п����ܵ�����Ħ���������� | |
| B�� | �ɦ�=$\frac{f}{N}$��֪����Ħ�������뻬��Ħ���������ȣ�����ѹ���ɷ��� | |
| C�� | Ħ�����ķ���������������˶������෴ | |
| D�� | Ħ�������Ƕ�������˶����谭���� |
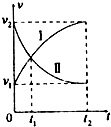 ��ͬһ�ص�ͬʱ��ʼ��ͬһֱ���˶�����������I��II���ٶ�ͼ����ͼ��ʾ����0��t2ʱ���ڣ�����˵������ȷ���ǣ�������
��ͬһ�ص�ͬʱ��ʼ��ͬһֱ���˶�����������I��II���ٶ�ͼ����ͼ��ʾ����0��t2ʱ���ڣ�����˵������ȷ���ǣ�������| A�� | ������������t1ʱ������ | |
| B�� | �����������ƽ���ٶȴ�С����$\frac{{{v_1}+{v_2}}}{2}$ | |
| C�� | �������������ܵĺ��������ڲ��ϼ�С | |
| D�� | ������ļ��ٶȲ�����������ļ��ٶȲ��ϼ�С |
 ��ͼ��ʾ���ڱڹ⻬�뾶��СΪR��Բ�����ֱ�̶��������ϣ�һ������Ϊm��С��ֹ�ڹ���ײ�A�㣮����С����ˮƽ������ٻ���С�����Ѹ���ƿ���ʹС���ع������ֱ�����˶�����С��ص�A��ʱ���ٴ���С�����˶��������С��ͨ�����λ���С������˶���Բ�������ߵ㣮��֪С�����˶�������ʼ��δ���������ڵ�һ�λ��������С����С������W1���ڶ��λ��������С����С������W2�����Ⱥ����λ��������С����С������ȫ����������С��Ķ��ܣ���$\frac{{W}_{1}}{{W}_{2}}$��ֵ�����ǣ�������
��ͼ��ʾ���ڱڹ⻬�뾶��СΪR��Բ�����ֱ�̶��������ϣ�һ������Ϊm��С��ֹ�ڹ���ײ�A�㣮����С����ˮƽ������ٻ���С�����Ѹ���ƿ���ʹС���ع������ֱ�����˶�����С��ص�A��ʱ���ٴ���С�����˶��������С��ͨ�����λ���С������˶���Բ�������ߵ㣮��֪С�����˶�������ʼ��δ���������ڵ�һ�λ��������С����С������W1���ڶ��λ��������С����С������W2�����Ⱥ����λ��������С����С������ȫ����������С��Ķ��ܣ���$\frac{{W}_{1}}{{W}_{2}}$��ֵ�����ǣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{3}{4}$ | D�� | 1 |
 ��ͼ��ʾ��һ������Ϊm�������+q�Ĵ��������������Բ��ƣ����Ӿ�ֹ��ʼ��U1��ѹ���ٺ�ˮƽ������ƽ�н�������ƫת�糡�У������峤L��������d�������ƫת�糡ʱ��ƫת�Ǧ�=30�㣬�ֽ��Ž���һ������ֱ��ֽ���������ǿ�ų�������
��ͼ��ʾ��һ������Ϊm�������+q�Ĵ��������������Բ��ƣ����Ӿ�ֹ��ʼ��U1��ѹ���ٺ�ˮƽ������ƽ�н�������ƫת�糡�У������峤L��������d�������ƫת�糡ʱ��ƫת�Ǧ�=30�㣬�ֽ��Ž���һ������ֱ��ֽ���������ǿ�ų������� ��·��ͼ���ף���ʾ����ֵ����R=3������Դ��·�˵�ѹU�����I�ı仯ͼ����ͼ���ң���ʾ���պϵ��S����
��·��ͼ���ף���ʾ����ֵ����R=3������Դ��·�˵�ѹU�����I�ı仯ͼ����ͼ���ң���ʾ���պϵ��S���� �̳�������Ա��������m=20kg��ľ����ˮƽ�����˶���������F1=100N��ˮƽ������ľ�䣬ľ��ǡ��������ֱ���˶����ָ���F2=150N����ˮƽ�����53��б���ϵ����������ھ�ֹ��ľ���ϣ���ͼ��ʾ����֪sin53��=0.80��cos53��=0.60��ȡ�������ٶ�g=10m/s2����
�̳�������Ա��������m=20kg��ľ����ˮƽ�����˶���������F1=100N��ˮƽ������ľ�䣬ľ��ǡ��������ֱ���˶����ָ���F2=150N����ˮƽ�����53��б���ϵ����������ھ�ֹ��ľ���ϣ���ͼ��ʾ����֪sin53��=0.80��cos53��=0.60��ȡ�������ٶ�g=10m/s2���� �����ֱ�Ϊm1=2kg��m2=1kg������С���ڹ⻬��ˮƽ���Ϸ��ٶ�v1=2m/s��v2=1m/sͬ���˶�������������ײ������m2���Ҳ��ǽԭ�ٵ��أ�����m1��������������ֹ���������һ������m1����ٶȴ�С��
�����ֱ�Ϊm1=2kg��m2=1kg������С���ڹ⻬��ˮƽ���Ϸ��ٶ�v1=2m/s��v2=1m/sͬ���˶�������������ײ������m2���Ҳ��ǽԭ�ٵ��أ�����m1��������������ֹ���������һ������m1����ٶȴ�С�� ��ͼ��ʾ��һ���������������尴p-Tͼ���м�ͷ����״̬A�仯��״̬B���ٱ仯��״̬C����֪������״̬Aʱ�����Ϊ33.6L��
��ͼ��ʾ��һ���������������尴p-Tͼ���м�ͷ����״̬A�仯��״̬B���ٱ仯��״̬C����֪������״̬Aʱ�����Ϊ33.6L��