题目内容
2.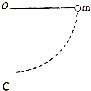 如图所示,质量为2m、电量为+q的带电小球A固定于一不可伸长的绝缘细线一端O点,绳的另一端有一电荷量为+Q质量为m的小球B,绳长为l,将小球拉起至与球A等高的位置后无初速度释放.
如图所示,质量为2m、电量为+q的带电小球A固定于一不可伸长的绝缘细线一端O点,绳的另一端有一电荷量为+Q质量为m的小球B,绳长为l,将小球拉起至与球A等高的位置后无初速度释放.(1)则小球B经过最低点C时的速度大小;
(2)则小球经过最低点C时绳受到的拉力.
分析 (1)从静止释放到C点,只有重力做功,由动能定理可求经过最低点C时的速度大小;
(2)由由牛顿第二定律可求小球经过最低点C时绳受到的拉力.
解答 解:(1)从静止释放,只有重力做功,由动能定理可得:mgl=$\frac{1}{2}$mvC2
解得:vC=$\sqrt{2gl}$
(2)在最低点,由牛顿第二定律可得:T-mg-k$\frac{Qq}{{l}^{2}}$=m$\frac{{v}_{C}^{2}}{l}$
解得绳子的拉力为:T=3mg+k$\frac{Qq}{{l}^{2}}$.
答:(1)小球B经过最低点C时的速度大小为$\sqrt{2gl}$;
(2)小球经过最低点C时绳受到的拉力为3mg+k$\frac{Qq}{{l}^{2}}$.
点评 解答此题的关键是知道从静止释放,小球受重力、静电力和绳子的拉力,但是只有重力做功;
在最低点小球受到的合力提供向心力.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
10. 欣欣和强强在打扫实验室时,发现实验桌上有一个灯泡,铭牌上标有“4V W”,其中W前面的数字不清楚了,欣欣很想知道它是多少,刚好桌上还有电阻箱、电流表、开关、12V的稳压电源各一个,欣欣用它们连成了如图所示的电路,测出电流表示数随电阻箱阻值变化的几组值并记录在表中.
欣欣和强强在打扫实验室时,发现实验桌上有一个灯泡,铭牌上标有“4V W”,其中W前面的数字不清楚了,欣欣很想知道它是多少,刚好桌上还有电阻箱、电流表、开关、12V的稳压电源各一个,欣欣用它们连成了如图所示的电路,测出电流表示数随电阻箱阻值变化的几组值并记录在表中.
问:(1)通过实验,欣欣发现灯泡的电阻是变化(填“不变”“变化”)的,这是因为随电流的减小灯丝温度降低,而使电阻阻值减小.
(2)强强也对欣欣的实验进行了研究,发现欣欣记录的数据中有一个电流值有错误,这个错误数据是0.20,请简要讲出你的判断依据.
(3)当电流为0.50A时,电阻箱两端的电压是多少?
(4)灯泡的铭牌上不清楚的数字是多少?(写出计算过程)
 欣欣和强强在打扫实验室时,发现实验桌上有一个灯泡,铭牌上标有“4V W”,其中W前面的数字不清楚了,欣欣很想知道它是多少,刚好桌上还有电阻箱、电流表、开关、12V的稳压电源各一个,欣欣用它们连成了如图所示的电路,测出电流表示数随电阻箱阻值变化的几组值并记录在表中.
欣欣和强强在打扫实验室时,发现实验桌上有一个灯泡,铭牌上标有“4V W”,其中W前面的数字不清楚了,欣欣很想知道它是多少,刚好桌上还有电阻箱、电流表、开关、12V的稳压电源各一个,欣欣用它们连成了如图所示的电路,测出电流表示数随电阻箱阻值变化的几组值并记录在表中.| 电流/A | 0.90 | 0.80 | 0.50 | 0.36 | 0.28 | 0.20 |
| 电阻/Ω | 8 | 10 | 20 | 30 | 40 | 50 |
(2)强强也对欣欣的实验进行了研究,发现欣欣记录的数据中有一个电流值有错误,这个错误数据是0.20,请简要讲出你的判断依据.
(3)当电流为0.50A时,电阻箱两端的电压是多少?
(4)灯泡的铭牌上不清楚的数字是多少?(写出计算过程)
14. 如图所示,在水平放置的两平行金属板之间、有场强为E的匀强电场和磁感强度为B的匀强磁场,有一束质量、电量、电性和运动速度均不相同的粒子(不计重力),沿水平方向射入,从挡板上的S小孔中穿出.( )
如图所示,在水平放置的两平行金属板之间、有场强为E的匀强电场和磁感强度为B的匀强磁场,有一束质量、电量、电性和运动速度均不相同的粒子(不计重力),沿水平方向射入,从挡板上的S小孔中穿出.( )
 如图所示,在水平放置的两平行金属板之间、有场强为E的匀强电场和磁感强度为B的匀强磁场,有一束质量、电量、电性和运动速度均不相同的粒子(不计重力),沿水平方向射入,从挡板上的S小孔中穿出.( )
如图所示,在水平放置的两平行金属板之间、有场强为E的匀强电场和磁感强度为B的匀强磁场,有一束质量、电量、电性和运动速度均不相同的粒子(不计重力),沿水平方向射入,从挡板上的S小孔中穿出.( )| A. | 当E=B时,所有粒子均能穿过S小孔 | |
| B. | 当υ>$\frac{E}{B}$时,所有粒子均打在S小孔的上部挡板 | |
| C. | 当υ<$\frac{E}{B}$时,所有粒子均打在S小孔的下部挡板 | |
| D. | 当υ=$\frac{E}{B}$时,所有粒子均能穿过S小孔 |
11.在图示的闭合电路中,当滑片P向右移动时,两电表读数的变化不正确的是( )


| A. |  变大, 变大, 变大 变大 | B. |  变小, 变小, 变大 变大 | C. |  变大, 变大, 变小 变小 | D. |  变小, 变小, 变小 变小 |
12. 如图所示,轻绳 AD 跨过固定在水平横梁 BC 右端的定滑轮挂住一个质量为0.1kg的物体,∠ACB=30°.g取10m/s 2,求滑轮所受弹力大小为( )
如图所示,轻绳 AD 跨过固定在水平横梁 BC 右端的定滑轮挂住一个质量为0.1kg的物体,∠ACB=30°.g取10m/s 2,求滑轮所受弹力大小为( )
 如图所示,轻绳 AD 跨过固定在水平横梁 BC 右端的定滑轮挂住一个质量为0.1kg的物体,∠ACB=30°.g取10m/s 2,求滑轮所受弹力大小为( )
如图所示,轻绳 AD 跨过固定在水平横梁 BC 右端的定滑轮挂住一个质量为0.1kg的物体,∠ACB=30°.g取10m/s 2,求滑轮所受弹力大小为( )| A. | 1N | B. | $\sqrt{3}$ N | C. | 2 N | D. | $\frac{\sqrt{3}}{2}$ N |
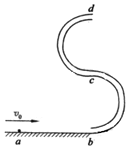 如图所示的“s”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,轨道在水平方向不可移动.弹射装置将一个小球(小球的直径略小于细圆管内径)从a点沿水平地面向b点运动并进入轨道,经过轨道后从最高点d水平抛出.已知小球与地面ab段间的动摩擦因数为μ,ab段长L,圆的半径R,小球质量m,求:
如图所示的“s”形玩具轨道,该轨道是用内壁光滑的薄壁细圆管弯成,放置在竖直平面内,轨道弯曲部分是由两个半径相等的半圆对接而成,圆半径比细管内径大得多,轨道底端与水平地面相切,轨道在水平方向不可移动.弹射装置将一个小球(小球的直径略小于细圆管内径)从a点沿水平地面向b点运动并进入轨道,经过轨道后从最高点d水平抛出.已知小球与地面ab段间的动摩擦因数为μ,ab段长L,圆的半径R,小球质量m,求: 如图所示,在绝缘水平面上的O点固定一正电荷,电荷量为Q,在离O点高度为r0的A处由静止释放一个带同种电荷、电荷量为q的液珠,液珠开始运动瞬间的加速度大小恰好为重力加速度g,沿竖直方向运动到距O点距离为2r0的B点(图中未画出)时,液珠的速度刚好为零.已知静电常量为k,两电荷均可看成点电荷,不计空气阻力.
如图所示,在绝缘水平面上的O点固定一正电荷,电荷量为Q,在离O点高度为r0的A处由静止释放一个带同种电荷、电荷量为q的液珠,液珠开始运动瞬间的加速度大小恰好为重力加速度g,沿竖直方向运动到距O点距离为2r0的B点(图中未画出)时,液珠的速度刚好为零.已知静电常量为k,两电荷均可看成点电荷,不计空气阻力. 如图所示,边长为L=0.20m的正方形金属线框,放在光滑,绝缘的水平面上,线框的总电阻为R=1.0Ω,有界匀强磁场方向垂直纸面向里,磁感应强 度大小为B=0.50T,线框的右边与磁场边界平行.现用一水平外力将线框以v=10m/s的速度匀速拉出磁场区域.求:
如图所示,边长为L=0.20m的正方形金属线框,放在光滑,绝缘的水平面上,线框的总电阻为R=1.0Ω,有界匀强磁场方向垂直纸面向里,磁感应强 度大小为B=0.50T,线框的右边与磁场边界平行.现用一水平外力将线框以v=10m/s的速度匀速拉出磁场区域.求: 在“探究弹力和弹簧伸长关系”的实验中,某实验小组将不同数量的钩码分别挂竖直弹簧下端,进行测量,根据实验所测数据,利用描点法描出了所持钩码的重力G与弹簧总长L的关系图象,根据图象回答以下问题:
在“探究弹力和弹簧伸长关系”的实验中,某实验小组将不同数量的钩码分别挂竖直弹簧下端,进行测量,根据实验所测数据,利用描点法描出了所持钩码的重力G与弹簧总长L的关系图象,根据图象回答以下问题: