题目内容
14.如图2所示,某同学设计一个气垫导轨装置验证动量守恒定律的实验: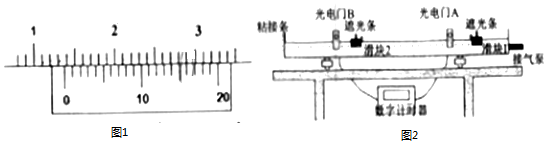
①用游标卡尺测得遮光条的宽度d如图1所示,则d=13.80mm;
②质量为m2的滑块2静止放在水平气垫导轨上光电门B的右侧,质量为m1的滑块从光电门A的右侧向左运动,穿过光电门A与滑块2发生碰撞,随后两个滑块分离并依次穿过光电门B,滑块2与导轨左端相碰并被粘接条粘住,待滑块1穿过光电门B后用手将它停住,两个滑块固定的遮光条宽度相同,数字计时器分别记录下滑块1通过光电门A的时间△t、滑块2和滑块1依次通过光电门B的时间△t2和△t1.本实验中两个滑块的质量大小关系应为m1>m2.若等式$\frac{{m}_{1}}{△{t}_{1}}$=$\frac{{m}_{1}}{△{t'}_{1}}$+$\frac{{m}_{2}}{△t{′}_{2}}$成立,则证明两滑块碰撞过程中系统的动量守恒(用题中的所给的字母表示).
分析 ①游标卡尺主尺与游标尺示数之和是游标卡尺示数;
②明确实验原理,根据动量守恒定律可分析应满足的表达式.
解答 解:①由图1所示游标卡尺可知,主尺示数为13mm,游标尺示数为16×0.05mm=0.80mm,游标卡尺示数为13mm+0.80mm=13.80mm;
②由题意可知,碰后要求两物体均沿A的原来运动方向运动,因此必须要求A的质量大于B的质量,即m1>m2;
根据平均速度公式可知,A的初速度v1=$\frac{d}{△t}$,碰后AB的速度分别为v1'=$\frac{d}{△{t}_{1}}$,v2'=$\frac{d}{△{t}_{2}}$;
根据动量守恒定律可知,应满足的表达式为:m1v1=m1v1'+m2v2'
将速度代入化简可知,只要满足:
$\frac{{m}_{1}}{△{t}_{1}}$=$\frac{{m}_{1}}{△{t'}_{1}}$+$\frac{{m}_{2}}{△t{′}_{2}}$
故答案为:①13.80;②m1>m2;$\frac{{m}_{1}}{△{t}_{1}}$=$\frac{{m}_{1}}{△{t'}_{1}}$+$\frac{{m}_{2}}{△t{′}_{2}}$
点评 本题考查验证动量守恒的实验,要注意明确实验原理,知道实验中的注意事项,能根据两物体的运动情况分析应满足的条件,同时注意求瞬时速度的方法.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
5.2016年1月20日,美国天文学家推测,太阳系有第九大行星,该行星质量约为地球的10倍,半径约为地球的4倍,绕太阳一周需约2万年,冥王星比它亮约一万倍.已知地球的半径为R,地球表面的重力加速度为g,引力常量为G,地球和该行星绕太阳运动均视为匀速圆周运动.下列说法正确的是( )
| A. | 太阳的质量约为$\frac{g{R}^{2}}{G}$ | |
| B. | 该行星的质量约为$\frac{10g{R}^{2}}{G}$ | |
| C. | 该行星表面的重力加速度约为$\frac{5}{8}$g | |
| D. | 该行星到太阳的距离约为地球到太阳的距离的7.4×102倍 |
2. 一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
 一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )
一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B.支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示.开始时OA边处于水平位置,由静止释放,则( )| A. | A球的最大速度为$2\sqrt{gl}$ | |
| B. | A球速度最大时,AB两球的总重力势能最小 | |
| C. | A球在向下运动的过程中机械能增大 | |
| D. | A、B两球的最大速度之比va:vb=2:1 |
4.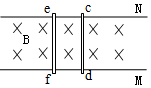 如图中M和N是两条在同一水平面内又互相平行的光滑金属导轨,ef和cd为两根金属棒,整个装置放在匀强磁场中,如果ef在外力作用下沿导轨向右运动,则通过cd的电流方向以及cd的运动方向是( )
如图中M和N是两条在同一水平面内又互相平行的光滑金属导轨,ef和cd为两根金属棒,整个装置放在匀强磁场中,如果ef在外力作用下沿导轨向右运动,则通过cd的电流方向以及cd的运动方向是( )
 如图中M和N是两条在同一水平面内又互相平行的光滑金属导轨,ef和cd为两根金属棒,整个装置放在匀强磁场中,如果ef在外力作用下沿导轨向右运动,则通过cd的电流方向以及cd的运动方向是( )
如图中M和N是两条在同一水平面内又互相平行的光滑金属导轨,ef和cd为两根金属棒,整个装置放在匀强磁场中,如果ef在外力作用下沿导轨向右运动,则通过cd的电流方向以及cd的运动方向是( )| A. | c到d,向右 | B. | d到c,向左 | C. | c到d,向左 | D. | d到c,向右 |
8. 光滑水平面上有一静止的木块,子弹水平射入木块后未穿出,子弹和木块的v-t图象如图所示,已知木块质量大于子弹质量,从子弹射入木块到达到隐定状态,已知木块增加了50J动能,则此过程产生的内能可能是( )
光滑水平面上有一静止的木块,子弹水平射入木块后未穿出,子弹和木块的v-t图象如图所示,已知木块质量大于子弹质量,从子弹射入木块到达到隐定状态,已知木块增加了50J动能,则此过程产生的内能可能是( )
 光滑水平面上有一静止的木块,子弹水平射入木块后未穿出,子弹和木块的v-t图象如图所示,已知木块质量大于子弹质量,从子弹射入木块到达到隐定状态,已知木块增加了50J动能,则此过程产生的内能可能是( )
光滑水平面上有一静止的木块,子弹水平射入木块后未穿出,子弹和木块的v-t图象如图所示,已知木块质量大于子弹质量,从子弹射入木块到达到隐定状态,已知木块增加了50J动能,则此过程产生的内能可能是( )| A. | 50J | B. | 70J | C. | 120J | D. | 180J |
9.我国第一颗月球探测卫星“嫦娥一号”已于2007年10月24日在西昌卫星发射中心由“长征三号甲”运载火箭成功发射升空.假设该卫星的绕月轨道是圆形的,且距离月球表面高度为h,并已知该卫星的运行周期为T,月球直径为d,万有引力常量为G,则可求出( )
| A. | 月球质量M=$\frac{{{π}^{2}(d+2h)}^{3}}{{2GT}^{2}}$ | |
| B. | 月球探测卫星“嫦娥一号”在离月球表面h高度轨道上运行的速度v=$\frac{πd}{T}$ | |
| C. | 月球探测卫星“嫦娥一号”绕月轨道的半径r=d+h | |
| D. | 月球表面的重力加速度g=$\frac{2πd}{{T}^{2}}$ |


 如图所示,光滑半圆轨道竖直放置,半径为R,一水平轨道与圆轨道相切,在水平光滑轨道上停着一个质量为M=0.99kg的木块,一颗质量为m=0.01kg的子弹,以vo=400m/s的水平速度射入木块中并未穿出,然后一起运动到轨道最高点(g取10m/s2),求:
如图所示,光滑半圆轨道竖直放置,半径为R,一水平轨道与圆轨道相切,在水平光滑轨道上停着一个质量为M=0.99kg的木块,一颗质量为m=0.01kg的子弹,以vo=400m/s的水平速度射入木块中并未穿出,然后一起运动到轨道最高点(g取10m/s2),求: 如图所示,在xoy平面的第一象限内加一垂直于纸面向外、磁感应强度为B的匀强磁场,一质量为m、带电荷量为q的正电粒子(重力不计)从坐标原点以速度v0射入第一象限,速度方向与x轴正向成37°角,粒子打在x轴上P点(图中未画出),若把磁场换为与xoy平面平行且与x轴正向成53°角斜向下的匀强方向,同一粒子仍从坐标原点以同一速度v0射入,粒子也打在P点,已知sin37°=0.6,cos37°=0.8,求:
如图所示,在xoy平面的第一象限内加一垂直于纸面向外、磁感应强度为B的匀强磁场,一质量为m、带电荷量为q的正电粒子(重力不计)从坐标原点以速度v0射入第一象限,速度方向与x轴正向成37°角,粒子打在x轴上P点(图中未画出),若把磁场换为与xoy平面平行且与x轴正向成53°角斜向下的匀强方向,同一粒子仍从坐标原点以同一速度v0射入,粒子也打在P点,已知sin37°=0.6,cos37°=0.8,求: