题目内容
8. 如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止开始做匀加速直线运动,下列结论正确的是( )
如图所示,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体从A点由静止开始做匀加速直线运动,下列结论正确的是( )| A. | $\frac{{x}_{AB}}{{{t}_{AB}}^{2}}$=$\frac{{x}_{AC}}{{{t}_{AC}}^{2}}$=$\frac{{x}_{AD}}{{{t}_{AD}}^{2}}$=$\frac{{x}_{AE}}{{{t}_{AE}}^{2}}$ | |
| B. | $\frac{{x}_{AB}}{{t}_{AB}}$=$\frac{{x}_{BC}}{{t}_{BC}}$=$\frac{{x}_{CD}}{{t}_{CD}}$=$\frac{{x}_{DE}}{{t}_{DE}}$ | |
| C. | tAB:tBC:tCD:tDE=1:($\sqrt{2}-1$):($\sqrt{3}-\sqrt{2}$):(2-$\sqrt{3}$) | |
| D. | vE=$\sqrt{2}$vB |
分析 根据匀变速直线运动的位移时间公式得出位移和时间的关系,根据初速度为零的匀加速直线运动的推论得出通过相等位移所用的时间之比.根据速度位移公式求出E点和B点的速度关系.
解答 解:A、根据x=$\frac{1}{2}a{t}^{2}$知,a=$\frac{2x}{{t}^{2}}$,则$a=\frac{{2x}_{AB}}{{{t}_{AB}}^{2}}=\frac{2{x}_{AC}}{{{t}_{AC}}^{2}}=\frac{2{x}_{AD}}{{{t}_{AD}}^{2}}=\frac{2{x}_{AE}}{{{t}_{AE}}^{2}}$,故A正确,B错误.
C、初速度为零的匀加速直线运动,在通过连续相等位移内的时间之比为1:($\sqrt{2}-1$):($\sqrt{3}-\sqrt{2}$):(2-$\sqrt{3}$),故C正确.
D、根据v2=2ax知,AE=4AB,则vE=2vB,故D错误.
故选:AC.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 为了测量某化肥厂的污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分辨为a、b、c,左右两端开口,在垂直于上下表面方向加磁感应强度为B的匀强磁场,在前后两个内侧面固定有金属板作为电极,污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U,若用Q表示污水流量(单位时间内排出的污水体积),下列说法正确的是( )
为了测量某化肥厂的污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分辨为a、b、c,左右两端开口,在垂直于上下表面方向加磁感应强度为B的匀强磁场,在前后两个内侧面固定有金属板作为电极,污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U,若用Q表示污水流量(单位时间内排出的污水体积),下列说法正确的是( )
 为了测量某化肥厂的污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分辨为a、b、c,左右两端开口,在垂直于上下表面方向加磁感应强度为B的匀强磁场,在前后两个内侧面固定有金属板作为电极,污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U,若用Q表示污水流量(单位时间内排出的污水体积),下列说法正确的是( )
为了测量某化肥厂的污水排放量,技术人员在该厂的排污管末端安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分辨为a、b、c,左右两端开口,在垂直于上下表面方向加磁感应强度为B的匀强磁场,在前后两个内侧面固定有金属板作为电极,污水充满管口从左向右流经该装置时,电压表将显示两个电极间的电压U,若用Q表示污水流量(单位时间内排出的污水体积),下列说法正确的是( )| A. | 前内侧面的电势一定低于后内侧面的电势,与哪种离子多无关 | |
| B. | 若污水中正离子较多,则前内侧面比后内侧面的电势高 | |
| C. | 污水中离子浓度越高,电压表的示数越大 | |
| D. | 污水流量Q与电压U成正比,与ab无关 |
19. 宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.
宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.
 宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.
宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为L,忽略其它星体对它们的引力作用,三颗星在同一平面内绕三角形中心O做匀速圆周运动,万有引力常量为G,下列说法正确的是.| A. | 每颗星做圆周运动的角速度为$\sqrt{\frac{3Gm}{{L}^{3}}}$ | |
| B. | 每颗星做圆周运动的加速度与三星的质量有关 | |
| C. | 若距离L和每颗星的质量m都变为原来的2倍,则周期变为原来的2倍 | |
| D. | 若距离L和每颗星的质量m都变为原来的2倍,则线速度变为原来的4倍 |
3.某物体运动的v-t图象如图所示,下列说法正确的是( )


| A. | 物体在5s内的位移大小为1m | |
| B. | 物体在6s末回到起点 | |
| C. | 物体在第2 s内和第3 s内的加速度是相同的 | |
| D. | 物体在第1 s末运动方向发生变化 |
8. 在x轴上存在与x轴平行的电场,x轴上各点的电势随x点位置变化情况如图所示.图中-x1~x1之间为曲线,且关于纵轴对称,其余均为直线,也关于纵轴对称.下列关于该电场的论述正确的是( )
在x轴上存在与x轴平行的电场,x轴上各点的电势随x点位置变化情况如图所示.图中-x1~x1之间为曲线,且关于纵轴对称,其余均为直线,也关于纵轴对称.下列关于该电场的论述正确的是( )
 在x轴上存在与x轴平行的电场,x轴上各点的电势随x点位置变化情况如图所示.图中-x1~x1之间为曲线,且关于纵轴对称,其余均为直线,也关于纵轴对称.下列关于该电场的论述正确的是( )
在x轴上存在与x轴平行的电场,x轴上各点的电势随x点位置变化情况如图所示.图中-x1~x1之间为曲线,且关于纵轴对称,其余均为直线,也关于纵轴对称.下列关于该电场的论述正确的是( )| A. | x轴上各点的场强大小相等 | |
| B. | 从-x1到x1场强的大小先减小后增大 | |
| C. | 一个带正电的粒子在x1点的电势能大于在-x1点的电势能 | |
| D. | 一个带负电的粒子在-x1点的电势能大于在-x2的电势能 |
 如图所示,质量为1kg的物块在倾角为53°的固定斜面上向下滑动,若给物块施加平行于斜面向上的拉力F,则物块刚好能匀速下滑,F=5N.求:物块与斜面之间的动摩擦因数.(sin53°=0.8,cos53°=0.6,g=10N/kg)
如图所示,质量为1kg的物块在倾角为53°的固定斜面上向下滑动,若给物块施加平行于斜面向上的拉力F,则物块刚好能匀速下滑,F=5N.求:物块与斜面之间的动摩擦因数.(sin53°=0.8,cos53°=0.6,g=10N/kg)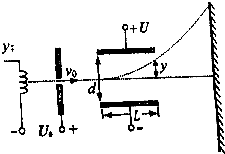 示波器是一种用途十分广泛的电子测量仪器,它的核心部件是示波管,其工作原理如图所示,初速为0的电子经过加速电压为U0的电场加速后,进入电压为U的偏转电场,然后射到荧光屏上.已知两偏转电极板间的距离为d,极板长为L,电子的质量为m,电荷量为e.不考虑电子所受重力,求:
示波器是一种用途十分广泛的电子测量仪器,它的核心部件是示波管,其工作原理如图所示,初速为0的电子经过加速电压为U0的电场加速后,进入电压为U的偏转电场,然后射到荧光屏上.已知两偏转电极板间的距离为d,极板长为L,电子的质量为m,电荷量为e.不考虑电子所受重力,求: