题目内容
17. 在某娱乐项目中,选手需借助悬挂在高处的绳飞跃到水面的浮台上,如图所示为其简化模型,设不可伸长的轻绳长为L,一质量为m的小球(可视为质点)摆到最低点后,绳子立即断裂,小球水平抛出.绳子的悬挂点O与水面间的距离为H.O点与浮台左端M的水平距离为s,浮台长也为s,厚度不计.若小球抛出后能落到浮台上,则小球抛出的速度范围为多少?
在某娱乐项目中,选手需借助悬挂在高处的绳飞跃到水面的浮台上,如图所示为其简化模型,设不可伸长的轻绳长为L,一质量为m的小球(可视为质点)摆到最低点后,绳子立即断裂,小球水平抛出.绳子的悬挂点O与水面间的距离为H.O点与浮台左端M的水平距离为s,浮台长也为s,厚度不计.若小球抛出后能落到浮台上,则小球抛出的速度范围为多少?
分析 小球摆到最低点时,绳子立即断裂,此后小球做平抛运动,已知水平距离和竖直高度,即可由平抛运动的规律求出小球抛出时的速度大小;
解答 解:要使使小球落到浮台上,则其水平位移应满足:
s≤x≤2s
由平抛运动公式有:
H-L=$\frac{1}{2}$gt2
若落点在M点:s=vt
解得:v=$\sqrt{\frac{g}{2(H-L)}}$s
若落到N点,则有v′=2$\sqrt{\frac{g}{2(H-L)}}$s;
答:小球抛出后能落到浮台上,则小球抛出的速度范围为($\sqrt{\frac{g}{2(H-L)}}$s,2$\sqrt{\frac{g}{2(H-L)}}$s)
点评 本题考查平抛运动的规律,要注意明确小球在竖直方向做自由落体运动,下落高度决定了飞行时间;水平方向做匀速运动,由匀速运动规律可求得速度.

练习册系列答案
相关题目
7. 如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自耦变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )
如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自耦变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )
 如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自耦变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )
如图所示,匝数为10的矩形线框处在磁感应强度B=$\sqrt{2}$T的匀强磁场中,绕垂直磁场的轴以恒定角速度ω=10rad/s在匀强磁场中转动,线框电阻不计,面积为0.4m2,线框通过滑环与一理想自耦变压器的原线圈相连,副线圈接有一只灯泡L(4W,100Ω)和滑动变阻器,已知图示状况下灯泡正常发光,电流表视为理想电表,则下列说法正确的是( )| A. | 此时原副线圈的匝数比为2:1 | |
| B. | 此时电流表的示数为0.4A | |
| C. | 若将自耦变压器触头向下滑动,灯泡会变亮 | |
| D. | 若将滑动变阻器滑片向上移动,则电流表示数增大 |
5.静止在粗糙水平面上的物体,在水平拉力F作用下做直线运动,其v-t图线如图所示,则( )


| A. | 在0-t1时间内.拉力F大小一定不断增大 | |
| B. | 在t1时刻,拉力F为零 | |
| C. | 在t1-t2时间内,拉力F大小可能不断减小 | |
| D. | 在t1-t2时间内,合力做功可能为零 |
12.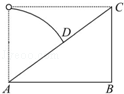 如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则DA与CD的比为( )
如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则DA与CD的比为( )
 如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则DA与CD的比为( )
如图,斜面AC与水平方向的夹角为α,在A点正上方与C等高处水平抛出一小球,其速度垂直斜面落到D点,则DA与CD的比为( )| A. | tanα | B. | 2tanα | C. | tan2α | D. | 2tan2α |
9. 如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,设两电极之间的电压大小为U,则( )
如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,设两电极之间的电压大小为U,则( )
 如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,设两电极之间的电压大小为U,则( )
如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,设两电极之间的电压大小为U,则( )| A. | U=$\frac{{{B^2}q{r^2}}}{2m}$ | B. | U=$\frac{{{B^2}q{r^2}}}{m}$ | C. | U=$\frac{{{B^{\;}}qr}}{m}$ | D. | U=$\frac{{\sqrt{2}{B^2}q{r^2}}}{2m}$ |
 如图所示,半径为R的绝缘光滑圆环固定在竖直平面内,环上套一质量为m且带正电荷的珠子,空间存在水平向右的匀强电场,珠子所受静电力是其重力的$\frac{3}{4}$倍,将珠子从环上最低位置A点静止释放.
如图所示,半径为R的绝缘光滑圆环固定在竖直平面内,环上套一质量为m且带正电荷的珠子,空间存在水平向右的匀强电场,珠子所受静电力是其重力的$\frac{3}{4}$倍,将珠子从环上最低位置A点静止释放. 如图所示,在竖直平面内,各轨道均为光滑轨道,圆形轨道的半径为R,质量为m的小物块从斜面上距水平面高h=2.5R的A点由静止开始下滑,物块通过轨道连接处的B、C点时,无机械能损失,求:
如图所示,在竖直平面内,各轨道均为光滑轨道,圆形轨道的半径为R,质量为m的小物块从斜面上距水平面高h=2.5R的A点由静止开始下滑,物块通过轨道连接处的B、C点时,无机械能损失,求: 如图所示,一定质量的理想气体从状态A变化到状态B,再从状态B变化到状态C,已知状态A的温度为480K,求:
如图所示,一定质量的理想气体从状态A变化到状态B,再从状态B变化到状态C,已知状态A的温度为480K,求: