题目内容
15.如图所示,可视为质点的木块A、B质量为mA=mB=2kg,两物体与水平地面的动摩擦因数均为μ=0.4,木块A、B粘在一起且中间夹有一小块炸药(炸药的质量可以忽略不计).当A、B向右运动到O点时速度为v0=1m/s,此时炸药爆炸使木块A、B分离,A运动距离L=1.5m后到达P点速度变为v=2m/s,炸药爆炸时释放的化学能均全部转化为木块的动能,爆炸时间很短可以忽略不计.重力加速度为g=10m/s2求:
(1)爆炸瞬间B的冲量;∵
(2)炸药爆炸时释放的化学能.
分析 (1)由牛顿第二定律求出A的加速度,应用匀变速直线运动的速度位移公式求出它的初速度,爆炸过程系统动量守恒,应用动量守恒定律求出B的速度,然后应用动量定理求出冲量.
(2)应用能量守恒定律可以求出爆炸过程释放的化学能.
解答 解:(1)对A,由牛顿第二定律得:-μmAg=mAa,
解得:a=4m/s2,
由匀变速直线运动的速度位移公式得:v2-v12=2aL,
解得:v1=4m/s,
爆炸过程系统动量守恒,以初速度方向为正方向,
由动量守恒定律得:(mA+mB)v0=mAv1+mBv2,
解得:v2=-2m/s,
爆炸过程,对B由动量定理得:I=mBv2-mBv0,
解得:I=-6N•s,方向:水平向左;
(2)爆炸过程,由能量守恒定律得:△EP=$\frac{1}{2}$mAv12+$\frac{1}{2}$mBv22-$\frac{1}{2}$(mA+mB)v02,
解得:△EP=18J;
答:(1)爆炸瞬间B的冲量大小为:6Ns,方向:水平向左;∵
(2)炸药爆炸时释放的化学能为18J.
点评 本题考查了求动摩擦因数、爆炸释放的化学能,分析清楚运动过程、应用动能定理、动量守恒定律、能量守恒定律即可正确解题,对于含有爆炸的过程,往往是动量守恒和能量守恒两大定律的综合应用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
5.一宇宙飞船绕地球做匀速圆周运动,飞船原来的线速度是v1,周期是T1,假设在某时刻它向前喷气做减速运动后,进入新轨道做匀速圆周运动,运动的线速度是v2,周期是T2,则( )
| A. | v1>v2,T1>T2 | B. | v1>v2,T1<T2 | C. | v1<v2,T1>T2 | D. | v1<v2,T1<T2 |
6. 如图是某探测器绕月球飞行的轨迹模拟图,A和B是椭圆轨道上的两个位置,关于探测器在A、B位置受到月球的万有引力和速度大小,下列说法正确的是( )
如图是某探测器绕月球飞行的轨迹模拟图,A和B是椭圆轨道上的两个位置,关于探测器在A、B位置受到月球的万有引力和速度大小,下列说法正确的是( )
 如图是某探测器绕月球飞行的轨迹模拟图,A和B是椭圆轨道上的两个位置,关于探测器在A、B位置受到月球的万有引力和速度大小,下列说法正确的是( )
如图是某探测器绕月球飞行的轨迹模拟图,A和B是椭圆轨道上的两个位置,关于探测器在A、B位置受到月球的万有引力和速度大小,下列说法正确的是( )| A. | A点的万有引力较大,B点的速率较大 | |
| B. | A点的万有引力较大,B点的速率较小 | |
| C. | A点的万有引力较小,B点的速率较大 | |
| D. | A点的万有引力较小,B点的速率较小 |
10.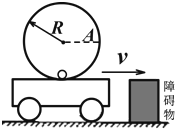 如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
 如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )| A. | 铅球能上升的最大高度一定等于$\frac{{v}^{2}}{2g}$ | |
| B. | 无论v多大,铅球上升的最大高度不超过$\frac{{v}^{2}}{2g}$ | |
| C. | 要使铅球一直不脱离圆桶,v的最小速度为$\sqrt{5gR}$ | |
| D. | 若铅球能到达圆桶最高点,则铅球在最高点的速度大小可以等于零 |
20. 如图所示,物体M放置于倾角为θ的斜面上,在平行于斜面的水平拉力F的作用下处于静止状态,如过将外力F撤去,则与撤去F之前比较,物体所受的摩擦力( )
如图所示,物体M放置于倾角为θ的斜面上,在平行于斜面的水平拉力F的作用下处于静止状态,如过将外力F撤去,则与撤去F之前比较,物体所受的摩擦力( )
 如图所示,物体M放置于倾角为θ的斜面上,在平行于斜面的水平拉力F的作用下处于静止状态,如过将外力F撤去,则与撤去F之前比较,物体所受的摩擦力( )
如图所示,物体M放置于倾角为θ的斜面上,在平行于斜面的水平拉力F的作用下处于静止状态,如过将外力F撤去,则与撤去F之前比较,物体所受的摩擦力( )| A. | 大小和方向均改变 | B. | 大小不变,方向改变 | ||
| C. | 大小改变,方向不变 | D. | 大小和方向均不改变 |
20.关于动能定理,下列说法中正确的是( )
| A. | 某过程中外力的总功等于各力做功的代数和 | |
| B. | 只要合外力对物体做了功,物体的动能就一定改变 | |
| C. | 在物体动能不改变的过程中,动能定理不适用 | |
| D. | 动能定理只适用于受恒力作用而加速运动的过程 |
1.如图所示是某物体运动的v-t图象,则下列说法正确的是( )


| A. | 前2s和后3s内物体的加速度大小均不变 | |
| B. | 2~5s内物体静止 | |
| C. | 前2s和后3s内速度的变化量为5m/s | |
| D. | 前2s的加速度为2.5m/s2,后3s的加速度为$-\frac{5}{3}$m/s2 |

 嘉年华上有一种回力球游戏,如图所示,A、B分别为一固定在竖直平面内的光滑半圆形轨道的最高点和最低点,半圆形轨道的半径为2h,B点距水平地面的高度为h,某人在水平地面C点处以某一初速度抛出一个质量为m的小球,小球恰好水平进入半圆轨道内侧的最低点B,并恰好能过最高点A后水平抛出,若不计空气阻力,已知当地重力加速度为g,求:
嘉年华上有一种回力球游戏,如图所示,A、B分别为一固定在竖直平面内的光滑半圆形轨道的最高点和最低点,半圆形轨道的半径为2h,B点距水平地面的高度为h,某人在水平地面C点处以某一初速度抛出一个质量为m的小球,小球恰好水平进入半圆轨道内侧的最低点B,并恰好能过最高点A后水平抛出,若不计空气阻力,已知当地重力加速度为g,求: