题目内容
10.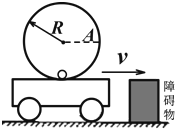 如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )
如图所示,半径为R、内壁光滑的硬质小圆桶固定在小车上,小车以速度v在光滑的水平公路上做匀速运动,有一质量为m、可视为质点的光滑小铅球在小圆桶底端与小车保持相对静止.当小车与固定在地面的障碍物相碰后,小车的速度立即变为零.关于碰后的运动(小车始终没有离开地面),下列说法正确的是( )| A. | 铅球能上升的最大高度一定等于$\frac{{v}^{2}}{2g}$ | |
| B. | 无论v多大,铅球上升的最大高度不超过$\frac{{v}^{2}}{2g}$ | |
| C. | 要使铅球一直不脱离圆桶,v的最小速度为$\sqrt{5gR}$ | |
| D. | 若铅球能到达圆桶最高点,则铅球在最高点的速度大小可以等于零 |
分析 小球与车原来有共同速度,当小车遇到障碍物突然停止后,小球由于惯性会继续运动,冲上圆弧槽,有两种可能:一是速度较小,滑到某处速度为0,由机械能守恒定律分析最大高度.另一可能速度较大,小球通过到达圆弧最高点做完整的圆周运动,或没有到达最高点就离开弧面而做斜抛运动,再由机械能守恒定律和斜抛的规律分析最大高度.
解答 解:AB、小球与车原来有共同速度,当小车遇到障碍物突然停止后,小球由于惯性会继续运动,冲上圆弧槽,有两种可能:一是速度较小,滑到某处速度为0,由机械能守恒定律有:
$\frac{1}{2}m{v}^{2}$=mgh,解得,最大高度 h=$\frac{{v}^{2}}{2g}$;
另一可能速度较大,小球通过到达圆弧最高点做完整的圆周运动,或没有到达最高点就离开弧面而做斜抛运动,则在最高点还有水平速度,由机械能守恒定律可知小球所能达到的最大高度要小于$\frac{{v}^{2}}{2g}$,故A错误,B正确.
C、要使铅球一直不脱离圆桶,则在最高点重力完全充当向心力,故有 mg=m$\frac{v{′}^{2}}{R}$,此时小球最高点的最小速度为 v′=$\sqrt{gR}$.
从最低点到最高点,由机械能守恒定律有 mg•2R=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}mv{′}^{2}$,解得 v=$\sqrt{5gR}$,即要使铅球一直不脱离圆桶,v的最小速度为$\sqrt{5gR}$,故C正确.
D、由上分析知,铅球能到达圆桶最高点,则铅球在最高点的速度大小最小为$\sqrt{gR}$.故D错误.
故选:BC
点评 本题的关键要知道铅球在最高点的临界条件:重力等于向心力,临界速度为$\sqrt{gR}$.要掌握斜抛运动的规律,知道斜抛最高点有水平速度,运用机械能守恒定律和牛顿第二定律结合分析这类问题.

 如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )
如图所示为“割绳子”游戏中的一幅截图,游戏中割断左侧绳子糖果就会通过正下方第一颗星星,糖果一定能经过星星处吗?现将其中的物理问题抽象出来进行研究:三根不可伸长的轻绳共同系住一颗质量为m的糖果(可视为质点),设从左到右三根轻绳的长度分别为l1、l2和l3,其中最左侧的绳子处于竖直且张紧的状态,另两根绳均处于松弛状态,三根绳的上端分别固定在同一水平线上,且相邻两悬点间距离均为d,糖果正下方的第一颗星星与糖果距离为h.已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零,现将最左侧的绳子割断,以下选项正确的是( )| A. | 只要满足l2≥$\sqrt{({l}_{1}+h)^{2}+{d}^{2}}$,糖果就能经过正下方第一颗星星处 | |
| B. | 只要满足l3≥$\sqrt{({l}_{1}+h)^{2}+4{d}^{2}}$,糖果就能经过正下方第一颗星星处 | |
| C. | 糖果可能以$\frac{mg{{l}_{2}}^{2}}{{d}^{2}}$($\sqrt{{{l}_{2}}^{2}-{d}^{2}}$-l1)的初动能开始绕中间悬点做圆运动 | |
| D. | 糖果到达最低点的动能可能等于mg[l2-$\frac{({{l}_{2}}^{2}-{d}^{2})^{\frac{3}{2}}}{{{l}_{2}}^{2}}$-$\frac{{l}_{1}{d}^{2}}{{{l}_{2}}^{2}}$] |
| A. | 地球引力对卫星不做功 | B. | 卫星的速度越来越大 | ||
| C. | 卫星受到的地球引力越来越小 | D. | 卫星受到的地球引力越来越大 |
 如图所示,在光滑的水平桌面上有一长为L=2m的木板C,它的两端各有一块挡板.C的质量为mC=5kg,在C的中央并排放着两个可视为质点的滑块A与B,其质量分别为mA=1kg、mB=4kg,开始时A、B、C均处于静止状态,并且A、B间夹有少许炸药,炸药爆炸使得A以vA=6m/s的速度水平向左运动,设堡寨释放的化学能全部转化为机械能,不计一切摩擦,两滑块中任一块与挡板碰撞后就与挡板合成一体,爆炸与碰撞时间不计,求:
如图所示,在光滑的水平桌面上有一长为L=2m的木板C,它的两端各有一块挡板.C的质量为mC=5kg,在C的中央并排放着两个可视为质点的滑块A与B,其质量分别为mA=1kg、mB=4kg,开始时A、B、C均处于静止状态,并且A、B间夹有少许炸药,炸药爆炸使得A以vA=6m/s的速度水平向左运动,设堡寨释放的化学能全部转化为机械能,不计一切摩擦,两滑块中任一块与挡板碰撞后就与挡板合成一体,爆炸与碰撞时间不计,求:

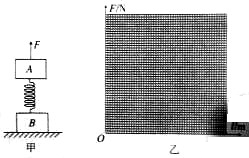 质量均为4kg的物体A、B用一劲度系数k=200N/m的轻质弹簧连接,将它们竖直静止放在水平面上,如图甲所示,现将一竖直向上的变力F作用在A上,使A开始向上做匀加速运动,经0.40s物体B刚要离开地面.取g=10m/s2
质量均为4kg的物体A、B用一劲度系数k=200N/m的轻质弹簧连接,将它们竖直静止放在水平面上,如图甲所示,现将一竖直向上的变力F作用在A上,使A开始向上做匀加速运动,经0.40s物体B刚要离开地面.取g=10m/s2 在“研究电磁感应现象“”的实验中.
在“研究电磁感应现象“”的实验中.