��Ŀ����
13�� ��ͼ��ʾ�������ǹ���ԭ����ʾ��ͼ����������a��b����ѹU���٣���A����ٶ�Ϊ0����ֱ����Ÿ�Ӧǿ�ȴ�СΪB������ֱ��ֽ�����ǿ�ų��У������ڴų���������Բ���˶������ֱ���ڸй��S�ϵ�x1��x2����ͼ�а�Բ�ε����߷ֱ��ʾ��������a��b��ͨ����·�������ƴ������ӵ�������������
��ͼ��ʾ�������ǹ���ԭ����ʾ��ͼ����������a��b����ѹU���٣���A����ٶ�Ϊ0����ֱ����Ÿ�Ӧǿ�ȴ�СΪB������ֱ��ֽ�����ǿ�ų��У������ڴų���������Բ���˶������ֱ���ڸй��S�ϵ�x1��x2����ͼ�а�Բ�ε����߷ֱ��ʾ��������a��b��ͨ����·�������ƴ������ӵ�������������| A�� | a������һ������b������ | B�� | a�ĵ����һ������b�ĵ���� | ||
| C�� | a�˶���ʱ�����b�˶���ʱ�� | D�� | a�ıȺɴ���b�ıȺ� |
���� ��������������ǿ�糡�����ȼ���ֱ���˶����ٽ���ų�������Բ���˶����켣Ϊ��Բ������ܶ�����ţ�ٵڶ�������⣮
��� �⣺A�������Ӿ��糡���ٺ���ٶȴ�СΪv���ų���Բ���˶��İ뾶Ϊr��������������ֱ�Ϊq��m�����ڸй���ϵľ���ΪS��
���ݶ��ܶ�������
qU=$\frac{1}{2}$mv2
��ã�v=$\sqrt{\frac{2qU}{m}}$
��qvB=m$\frac{{v}^{2}}{r}$
��ã�r=$\frac{mv}{qB}$=$\frac{1}{B}\sqrt{\frac{2mU}{q}}$
��S=2r=$\frac{2}{B}\sqrt{\frac{2mU}{q}}$
�õ���$\frac{q}{m}$=$\frac{8U}{B{S}^{2}}$
��ͼ��Sa��Sb��U��B��ͬ����$\frac{{q}_{a}}{{m}_{a}}$��$\frac{{q}_{b}}{{m}_{b}}$����D��ȷ��AB����
C���������ڹ�ʽT=$\frac{2��m}{Bq}$�������Ϸ�����֪���˶���ʱ��С��b�˶���ʱ�䣬��C����
��ѡ��D��
���� �������ڴ�����������ϳ����˶����⣬�糡�������ö������ٶȣ��ų���Բ���˶������Ļ��������ǻ��켣��

��ϰ��ϵ�д�
�����Ŀ
4�� ��ͼ��ʾ��������ֵ����R1��R2��������������ѹ��Ϊ12V��ֱ����Դ�ϣ����˰�һ�����費��Զ����R1��R2�ĵ�ѹ������R1���ˣ���ͼ������ѹ����ʾ��Ϊ4V��������Ѵ˵�ѹ���Ľ���R2���ˣ����ѹ����ʾ��һ���ᣨ������
��ͼ��ʾ��������ֵ����R1��R2��������������ѹ��Ϊ12V��ֱ����Դ�ϣ����˰�һ�����費��Զ����R1��R2�ĵ�ѹ������R1���ˣ���ͼ������ѹ����ʾ��Ϊ4V��������Ѵ˵�ѹ���Ľ���R2���ˣ����ѹ����ʾ��һ���ᣨ������
 ��ͼ��ʾ��������ֵ����R1��R2��������������ѹ��Ϊ12V��ֱ����Դ�ϣ����˰�һ�����費��Զ����R1��R2�ĵ�ѹ������R1���ˣ���ͼ������ѹ����ʾ��Ϊ4V��������Ѵ˵�ѹ���Ľ���R2���ˣ����ѹ����ʾ��һ���ᣨ������
��ͼ��ʾ��������ֵ����R1��R2��������������ѹ��Ϊ12V��ֱ����Դ�ϣ����˰�һ�����費��Զ����R1��R2�ĵ�ѹ������R1���ˣ���ͼ������ѹ����ʾ��Ϊ4V��������Ѵ˵�ѹ���Ľ���R2���ˣ����ѹ����ʾ��һ���ᣨ������| A�� | С��4V | B�� | ����4V | C�� | С��8V | D�� | ����8V |
8����ͼ��ʾ��������ͬ�ĵ���a��b��c�͵��費����ȦL�����費�Ƶ�Դ���ӣ������ж���ȷ���У�������


| A�� | K�պϵ�˲�䣬b��c�������Ȳ�ͬ | |
| B�� | K�պ��㹻����ʱ���Ժ�b��c����������ͬ | |
| C�� | K�Ͽ���˲�䣬a��c��������Ϩ�� | |
| D�� | K�Ͽ�֮��b��ͻȻ�����Ժ����䰵 |
18������˵������ȷ���ǣ�������
| A�� | �¶ȸߵ��������ܴ� | |
| B�� | ijϵͳ����������ͬʱ��������ȣ���ϵͳ�������п������� | |
| C�� | �������е�һ��Դ����������ȫ�������������������������仯 | |
| D�� | ���������Է����ɵ������崫���������� |
5�� A��B����Ȧ��ͬ�����ĵ����Ƴ���������ͬ�������뾶rA=2rB��������߽����ǿ�ų�ǡ��B��Ȧ�ڣ���ͼ��ʾ�����Ÿ�Ӧǿ�Ⱦ��ȼ�Сʱ����A��B����Ȧ����Ӱ�죬������
A��B����Ȧ��ͬ�����ĵ����Ƴ���������ͬ�������뾶rA=2rB��������߽����ǿ�ų�ǡ��B��Ȧ�ڣ���ͼ��ʾ�����Ÿ�Ӧǿ�Ⱦ��ȼ�Сʱ����A��B����Ȧ����Ӱ�죬������
 A��B����Ȧ��ͬ�����ĵ����Ƴ���������ͬ�������뾶rA=2rB��������߽����ǿ�ų�ǡ��B��Ȧ�ڣ���ͼ��ʾ�����Ÿ�Ӧǿ�Ⱦ��ȼ�Сʱ����A��B����Ȧ����Ӱ�죬������
A��B����Ȧ��ͬ�����ĵ����Ƴ���������ͬ�������뾶rA=2rB��������߽����ǿ�ų�ǡ��B��Ȧ�ڣ���ͼ��ʾ�����Ÿ�Ӧǿ�Ⱦ��ȼ�Сʱ����A��B����Ȧ����Ӱ�죬������| A�� | A��B�����в����ĸ�Ӧ�綯��֮��Ϊ4��1 | |
| B�� | A��B�����в����ĸ�Ӧ����֮��Ϊ2��1 | |
| C�� | A��B�����в����ĸ�Ӧ����֮��Ϊ1��2 | |
| D�� | A���в�������Ÿ�Ӧ����B�����и�Ӧ���� |
2����֪����뾶ΪR������ΪM�����渽�����������ٶ�Ϊg��������������ΪG����ô��һ�����ٶȵı���ʽ����СΪ��������
| A�� | $\sqrt{\frac{R}{g}}$ | B�� | $\sqrt{\frac{GM}{R}}$ | C�� | 7.9km/s | D�� | 11.2km/s |
 ����ΪL=0.4m��һ�˹̶�һС����һ�˹̶���ת����O�ϣ�С����������ֱƽ����ת�����˵��������Բ��ƣ�С�������Ϊ0.5kg����g=10m/s2����
����ΪL=0.4m��һ�˹̶�һС����һ�˹̶���ת����O�ϣ�С����������ֱƽ����ת�����˵��������Բ��ƣ�С�������Ϊ0.5kg����g=10m/s2����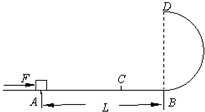 ��ͼ��ʾ���̶�����ֱ���ڵĹ⻬��Բ�ι����ֲ�ˮƽ�����B��ƽ�����ӣ�����뾶R=0.5m��һ����m=0.2kg��С��飨����Ϊ�ʵ㣩����ˮƽ����ϵ�A�㣬A��B���L=10m�������ˮƽ�����Ķ�Ħ��������=0.1������һˮƽ����F��������飮��֪F=3N��������˶���C��ʱ��ȥ��������C�㵽A��ľ���Ϊx����Բ�������ߵ�D����װһѹ����������������˶���D��ʱ�������ͻ���ʾ��Ӧ�Ķ���FN��ѹ�����������ܳ��ܵ����ѹ��Ϊ90N��gȡ10m/s2����Ҫʹ����ܹ�ͨ��Բ�������ߵ�D����x�ķ�Χ��
��ͼ��ʾ���̶�����ֱ���ڵĹ⻬��Բ�ι����ֲ�ˮƽ�����B��ƽ�����ӣ�����뾶R=0.5m��һ����m=0.2kg��С��飨����Ϊ�ʵ㣩����ˮƽ����ϵ�A�㣬A��B���L=10m�������ˮƽ�����Ķ�Ħ��������=0.1������һˮƽ����F��������飮��֪F=3N��������˶���C��ʱ��ȥ��������C�㵽A��ľ���Ϊx����Բ�������ߵ�D����װһѹ����������������˶���D��ʱ�������ͻ���ʾ��Ӧ�Ķ���FN��ѹ�����������ܳ��ܵ����ѹ��Ϊ90N��gȡ10m/s2����Ҫʹ����ܹ�ͨ��Բ�������ߵ�D����x�ķ�Χ��