题目内容
16.卫星围绕地球做近地运转,地球半径为R,卫星的运转周期为T,引力常量为G,则地球的密度的表达式$\frac{3π}{G{T}^{2}}$.分析 近地卫星绕地球做匀速圆周运动,根据万有引力提供向心力,可得地球质量,再结合体积表达式可得地球密度.
解答 解:近地卫星绕地球做匀速圆周运动,根据万有引力提供向心力得:
$G\frac{Mm}{{R}^{2}}=m\frac{4{π}^{2}R}{{T}^{2}}$
解得:M=$\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}$,
地球的体积为V=$\frac{4}{3}π{R}^{3}$,
则地球的密度$ρ=\frac{M}{V}=\frac{\frac{4{π}^{2}{R}^{3}}{G{T}^{2}}}{\frac{4}{3}π{R}^{3}}$=$\frac{3π}{G{T}^{2}}$.
故答案为:$\frac{3π}{G{T}^{2}}$
点评 解决本题的关键掌握万有引力提供向心力公式,知道近地卫星绕地球做匀速圆周运动的半径即为地球半径,难度适中.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
1.假设在半径为R的某天体发射一颗该天体的卫星,若它贴近天体的表面做匀速圆周运动的周期为T,已知引力常量为G,该天体表面的重力加速度为g,不考虑天体自转的影响.下列关于该天体密度ρ正确的是( )
| A. | ρ=$\frac{3π}{G{T}^{2}}$ | B. | ρ=$\frac{3π}{GT}$ | C. | ρ=$\frac{3g}{4πRG}$ | D. | ρ=$\frac{g}{4πRG}$ |
8.下面说法中正确的是( )
| A. | 库仑利用扭秤实验测量出了万有引力常量G的大小 | |
| B. | 法拉第第一次发现电流的磁效应,并且制成了发电机 | |
| C. | 机械波在不同的介质中传播其频率不会发生改变 | |
| D. | 波长比障碍物尺寸小或相差不多时,会发生明显衍射现象 |
6.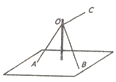 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
 如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )
如图所示,三根轻绳系于竖直杆上的同一点O,其中轻绳OA与OB等长且夹角为60°,竖直杆与平面AOB所成的角为30°.若轻绳OA、OB的拉力均为40N,要使杆受到绳子作用力的方向竖直向下,则水平轻绳OC的拉力大小为:( )| A. | 20$\sqrt{3}$N | B. | 40N | C. | 40$\sqrt{3}$N | D. | 60N |
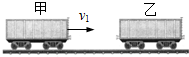 在列车编组站里,一辆m1=3.6×104kg的甲货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.4×104kg的静止的乙货车,它们碰撞后结合在一起继续运动,求货车碰撞后运动的速度以及甲货车在碰撞过程中动量的变化量.
在列车编组站里,一辆m1=3.6×104kg的甲货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.4×104kg的静止的乙货车,它们碰撞后结合在一起继续运动,求货车碰撞后运动的速度以及甲货车在碰撞过程中动量的变化量.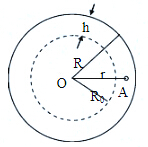 新发现行星,其星球半径为R=6400km,且由通常的水形成的海洋覆盖着它的所有表面,海洋的深度为h=10km,学者们对该行星进行探测时发现,当把试验用的样品浸入行星海洋的不同深度时,各处的自由落体加速度以相当高的精确度保持不变,已知万有引力常量G=6.67×10-11N•m2/kg2,海水密度ρ=1.0×103kg/m3,半径为R的球面面积公式S=4πR2.
新发现行星,其星球半径为R=6400km,且由通常的水形成的海洋覆盖着它的所有表面,海洋的深度为h=10km,学者们对该行星进行探测时发现,当把试验用的样品浸入行星海洋的不同深度时,各处的自由落体加速度以相当高的精确度保持不变,已知万有引力常量G=6.67×10-11N•m2/kg2,海水密度ρ=1.0×103kg/m3,半径为R的球面面积公式S=4πR2.