题目内容
1.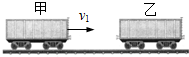 在列车编组站里,一辆m1=3.6×104kg的甲货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.4×104kg的静止的乙货车,它们碰撞后结合在一起继续运动,求货车碰撞后运动的速度以及甲货车在碰撞过程中动量的变化量.
在列车编组站里,一辆m1=3.6×104kg的甲货车在平直轨道上以v1=2m/s的速度运动,碰上一辆m2=2.4×104kg的静止的乙货车,它们碰撞后结合在一起继续运动,求货车碰撞后运动的速度以及甲货车在碰撞过程中动量的变化量.
分析 在碰撞现象中,相互作用时间很短,平均作用力很大,把相互碰撞的物体作为一个系统来看待,认为碰撞过程中动量守恒.两辆货车在碰撞前后,根据系统动量守恒列式求解.
解答 解:对整个系统,碰撞过程动量守恒,设结合在一起继续运动的速度为v.取向右为正方向,由动量守恒定律得:
则 m1v1=(m1+m2)v
解得,货车碰撞后运动的速度 $v=\frac{{{m_1}{v_1}}}{{({m_1}+{m_2})}}=1.2$m/s
甲货车的动量的变化量 $△p={m_1}v-{m_1}{v_1}=-2.88×{10^4}$kg•m/s
答:货车碰撞后运动的速度是1.2m/s,甲货车在碰撞过程中动量的变化量大小为2.88×104kg•m/s,方向向左.
点评 本题以火车挂钩这一实际问题为情景,涉及碰撞过程中的动量守恒定律的应用,用动量守恒定律解题时要注意矢量性(方向性),即表达式中的速度、动量均为矢量,在作用前后速度都在一条直线上的条件下,选定一个正方向,将矢量运算转化为代数运算.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
11.长为l的细绳一端固定,另一端系一个小球,使球在竖直平面内做圆周运动,那么正确的是( )


| A. | 小球通过圆周上顶点时的速度最小可以等于零 | |
| B. | 小球通过圆周上顶点时的最大速度为$\sqrt{gl}$ | |
| C. | 小球通过圆周上最低点时,小球需要的向心力最大 | |
| D. | 小球通过圆周上最低点时绳的张力最大 |
13. 如图所示,人沿平直的河岸以v匀速行走,且通过不可伸长的绳拖船,船沿绳的方向行进,此过程中绳始终与水面平行.则下列说法正确的是( )
如图所示,人沿平直的河岸以v匀速行走,且通过不可伸长的绳拖船,船沿绳的方向行进,此过程中绳始终与水面平行.则下列说法正确的是( )
 如图所示,人沿平直的河岸以v匀速行走,且通过不可伸长的绳拖船,船沿绳的方向行进,此过程中绳始终与水面平行.则下列说法正确的是( )
如图所示,人沿平直的河岸以v匀速行走,且通过不可伸长的绳拖船,船沿绳的方向行进,此过程中绳始终与水面平行.则下列说法正确的是( )| A. | 船在靠岸前做的是匀变速运动 | |
| B. | 船在靠岸前的运动轨迹是直线 | |
| C. | 当绳与河岸的夹角为α时,船的速率为vcosα | |
| D. | 当绳与河岸的夹角为α时,船的速率为$\frac{v}{cosα}$ |
 如图所示,放置在竖直平面内的$\frac{1}{4}$圆轨道AB,O点为圆心,OA水平,OB竖直,半径为2$\sqrt{2}$m.在O点沿OA抛出一小球,小球击中圆弧AB上的中点C,vt的反向延长线与OB的延长线相交于D点.已知重力加速度g=10m/s2.求:
如图所示,放置在竖直平面内的$\frac{1}{4}$圆轨道AB,O点为圆心,OA水平,OB竖直,半径为2$\sqrt{2}$m.在O点沿OA抛出一小球,小球击中圆弧AB上的中点C,vt的反向延长线与OB的延长线相交于D点.已知重力加速度g=10m/s2.求: 为了研究光通过折射率n=1.6的球形玻璃的偏折现象,让一细束光线射入玻璃球,玻璃球的半径R=10mm,球心O到入射光线的垂直距离d=8mm.( sin 53°=0.8 )
为了研究光通过折射率n=1.6的球形玻璃的偏折现象,让一细束光线射入玻璃球,玻璃球的半径R=10mm,球心O到入射光线的垂直距离d=8mm.( sin 53°=0.8 ) 图示电路中,电源为恒流源,能始终提供大小恒定的电流.R0为定值电阻,移动滑动变阻器的滑片,则下列表示电压表示数U、电路总功率P随电流表示数I变化的关系图线中,可能正确的是( )
图示电路中,电源为恒流源,能始终提供大小恒定的电流.R0为定值电阻,移动滑动变阻器的滑片,则下列表示电压表示数U、电路总功率P随电流表示数I变化的关系图线中,可能正确的是( )




 一个物体从光滑斜面Eh=1.8m的A点处由静止滑下,然后在粗糙水平面上滑行一段距离后停止,如图所示,不考虑物体滑至斜面底端的碰撞作用,设水平面与物体间的动摩擦因数为μ=0.2.若选择水平面为零势能面,则:
一个物体从光滑斜面Eh=1.8m的A点处由静止滑下,然后在粗糙水平面上滑行一段距离后停止,如图所示,不考虑物体滑至斜面底端的碰撞作用,设水平面与物体间的动摩擦因数为μ=0.2.若选择水平面为零势能面,则: