题目内容
9.据报道,“嫦娥一号”在距离月球表面高为h处绕月球做匀速圆周运动.已知月球半径为R,引力常量为G,求:(1)如果已知“嫦娥一号”的线速度为V,求月球的质量;
(2)如果已知月球表面的重力加速度为g0,求“嫦娥一号”绕月球运行的周期.
分析 (1)根据万有引力提供向心力速度公式求解月球质量;
(2)根据万有引力提供向心力周期公式结合在月球表面重力提供向心力公式联立方程求解.
解答 解:(1)由$G\frac{Mm}{(R+h)^{2}}=m\frac{{v}^{2}}{R+h}$得
月球的质量$M=\frac{{v}^{2}(R+h)}{G}$
(2)“嫦娥一号”绕月球做匀速圆周运动有
$G\frac{Mm}{{(R+h)}^{2}}=m\frac{4{π}^{2}(R+h)}{{T}^{2}}$ ①
在月球表面有${m}_{0}g=G\frac{M{m}_{0}}{{R}^{2}}$ ②
解①②得:$T=\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g}}$
答:(1)如果已知“嫦娥一号”的线速度为v,则月球的质量为$\frac{{v}^{2}(R+h)}{G}$;
(2)如果已知月球表面的重力加速度为g0,则“嫦娥一号”绕月球运行的周期为$\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g}}$.
点评 解决本题的关键掌握万有引力等于重力和万有引力提供向心力这两个理论,并能灵活运用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
17. 如图所示,一列横波沿x轴传播,t0时刻波的图象如图中实线所示.经△t=0.2s,波的图象如图中虚线所示.已知其波长为0.8m,则下述说法中正确的是( )
如图所示,一列横波沿x轴传播,t0时刻波的图象如图中实线所示.经△t=0.2s,波的图象如图中虚线所示.已知其波长为0.8m,则下述说法中正确的是( )
 如图所示,一列横波沿x轴传播,t0时刻波的图象如图中实线所示.经△t=0.2s,波的图象如图中虚线所示.已知其波长为0.8m,则下述说法中正确的是( )
如图所示,一列横波沿x轴传播,t0时刻波的图象如图中实线所示.经△t=0.2s,波的图象如图中虚线所示.已知其波长为0.8m,则下述说法中正确的是( )| A. | 若波向右传播,则波的周期可能大于2s | |
| B. | 若波向左传播,则波的周期可能大于0.2s | |
| C. | 若波向左传播,则波的波速可能小于7m/s | |
| D. | 若波速是19m/s,则波向右传播 |
4.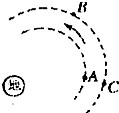 三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
 三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )
三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动,已知mA=mB<mC,则三颗卫星( )| A. | 线速度大小的关系是VA<VB=VC | |
| B. | 周期关系是TA>TB=TC | |
| C. | 向心力大小的关系是FA=FB<FC | |
| D. | 轨道半径和周期的关系是$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
14.2005年我国成功发射并回收了“神州”六号载人飞船.设飞船绕地球做匀速圆周运动,若飞船经历时间t绕地球运行n圈,则飞船离地面的高度为(已知地球半径为R,地面的重力加速度为g)( )
| A. | $\root{3}{\frac{g{R}^{2}{t}^{2}}{4{π}^{2}{n}^{2}}}$ | B. | $\root{3}{\frac{g{R}^{2}{t}^{2}}{4{π}^{2}{n}^{2}}}$-R | ||
| C. | $\root{3}{\frac{g{R}^{2}{t}^{2}}{{n}^{2}}}$ | D. | $\root{3}{\frac{g{R}^{2}{t}^{2}}{{n}^{2}}}$-R |
18.我国自行研制的“北斗”卫星导航定位系统需要发射35颗卫星,足足要比GPS多出11颗.按照规划,“北斗”卫星导航定位系统将有5颗静止轨道卫星和30颗非静止轨道卫星组成,采用“东方红”-3号卫星平台.30颗非静止轨道卫星又细分为27颗中轨道(MEO)卫星和3颗倾斜同步(IGSO)卫星组成,27颗MEO卫星平均分布在倾角55°的三个平面上,轨道高度21500公里.已知地球半径为6400km,自转周期为24h,地球表面的重力加速度为10m/s2.近似认为所有卫星都沿圆周轨道运动.由以上信息可知( )
| A. | 5颗静止轨道卫星都处于完全失重状态 | |
| B. | 27颗MEO卫星的运行速度大于静止轨道卫星的速度 | |
| C. | 27颗MEO卫星的运行周期大于24h | |
| D. | 地球球心一定在3颗倾斜同步(IGSO)卫星的轨道平面内 |
19.质点做匀速圆周运动时,下列说法正确的是( )
| A. | 速度的大小和方向都改变 | |
| B. | 匀速圆周运动是匀变速曲线运动 | |
| C. | 当物体做匀速圆周运动时,向心力就是所受合外力,所受合外力就是向心力 | |
| D. | 向心加速度大小不变,方向时刻改变 |
 如图所示,质量m=2kg的小物体P,在方向沿斜面向上,大小F=24N的拉力作用下,从斜面上的A点由静止起沿斜面向上做匀加速运动,物体与斜面间动摩擦因数μ=0.5,斜面的倾角为θ=37°,开始运动后5s末,撤去力F,再过5s,物体P到A点的距离是多少?(g取10m/s2,sin37°=0.6)
如图所示,质量m=2kg的小物体P,在方向沿斜面向上,大小F=24N的拉力作用下,从斜面上的A点由静止起沿斜面向上做匀加速运动,物体与斜面间动摩擦因数μ=0.5,斜面的倾角为θ=37°,开始运动后5s末,撤去力F,再过5s,物体P到A点的距离是多少?(g取10m/s2,sin37°=0.6)